Задачи линейного программирования
Математическая постановка экономических задач, связанных с управлением, может быть сформулирована в общем виде следующим образом [35].
Пусть имеется некоторая целевая функция 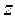 , которая зависит от параметров х=(
, которая зависит от параметров х=( 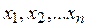 ), удовлетворяющих некоторым ограничениям
), удовлетворяющих некоторым ограничениям 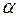 .
.
z = z(x,a).
Требуется найти такие значения параметров или функций х=( 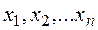 ), которые обращают величину
), которые обращают величину 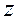 в максимум или минимум (то есть доставляют функции
в максимум или минимум (то есть доставляют функции 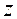 экстремум).
экстремум).
Такие задачи — отыскание значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, носят общее название задач математического программирования и решаются методами теории исследования операций.
Среди задач математического программирования самыми простыми являются задачи линейного программирования (ЗЛП). При этом оптимизируемая целевая функция z= z(x,a) линейно зависит от х=( 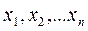 )и, кроме того, ограничения, накладываемые на х, имеют вид линейных равенств или неравенств.
)и, кроме того, ограничения, накладываемые на х, имеют вид линейных равенств или неравенств.
Замечание. В задачах нелинейного программирования целевая функция и ограничения содержат нелинейные выражения. Но здесь такие задачи не будут рассматриваться, поскольку очень многие практические задачи такого типа могут быть сведены к задачам линейного программирования, для которых разработано достаточное количество эффективных алгоритмов решений.
Основная задача линейного программирования (ОЗЛП) заключается в нахождении неотрицательных значений 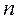 переменных
переменных 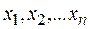 удовлетворяющих т условиям-равенствам:
удовлетворяющих т условиям-равенствам:
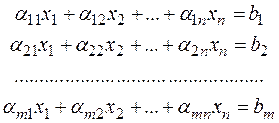
и обращающие в максимум линейную функцию (целевую функцию) этих переменных:
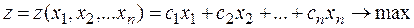
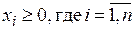
Допустимым решением (планом) ОЗЛП является упорядоченное множество значений 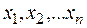 , удовлетворяющее ограничениям, показанным в приведённых равенствах.
, удовлетворяющее ограничениям, показанным в приведённых равенствах.
Допустимое решение, максимизирующее целевую функцию 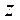 , называется оптимальным решением (оптимальным планом). Возможны случаи, когда оптимальное решение (если оно существует) является единственным или оптимальных решений бесчисленное множество.
, называется оптимальным решением (оптимальным планом). Возможны случаи, когда оптимальное решение (если оно существует) является единственным или оптимальных решений бесчисленное множество.
Дата добавления: 2015-10-13; просмотров: 1356;
