Этап С.
Для вывода итогового сообщения о результате решения используется диалоговое окно «Результаты поиска решения».
Диалоговое окно «Результаты поиска решения» содержит следующие поля:
«Сохранить найденное решение» - служит для сохранения найденного решения во влияющих ячейках модели.
«Восстановить исходные значения» — служит для восстановления исходных значений влияющих ячеек модели.
«Отчеты» — служит для указания типа отчета, размещаемого на отдельном листе книги.
«Результаты» - используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.
«Устойчивость» - используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле (поле «Установить целевую ячейку», диалоговое окно «Поиск решения») или в формулах ограничений.
«Ограничения» - используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.
«Сохранить сценарий» — служит для отображения диалогового окна Сохранение сценария, в котором можно сохранить сценарий решения задачи, чтобы использовать его в дальнейшем с помощью диспетчера сценариев MS Excel.
Одной из возможных задач и моделей линейной оптимизации является задача о планировании производства.
Предприятие должно производить изделия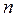 
видов: 
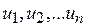, причем количество каждого выпускаемого изделия не должно превысить спрос 
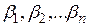и одновременно не должно быть меньше запланированных величин 
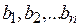соответственно. На изготовление изделий идет m видов сырья 
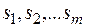, запасы которых ограничены соответственно величинами 
Известно, что на изготовление i-ro изделия идет 
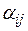единиц j-го сырья. Прибыль, получаемая от реализации изделий 
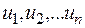равна соответственно 
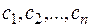. Требуется так спланировать производство изделий, чтобы прибыль была максимальной и при этом выполнялся план на производство каждого изделия, но не превышался спрос на него.
Аналитическая математическая модель. Обозначим через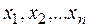 
количества единиц изделий 
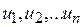, выпускаемых предприятием. Прибыль, приносимая планом (целевая функция), будет равна:
.
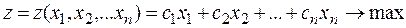Ограничения на выполнение плана запишется в виде: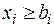 
для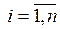 
. Чтобы не превысить спрос, надо ограничить выпуск изделий: 
для 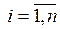. И, наконец, ограничения на сырье запишутся в виде системы неравенств:
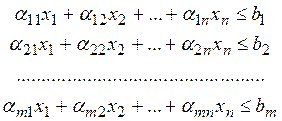
при условии, что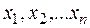 
неотрицательны.
Дата добавления: 2015-10-13; просмотров: 705;