Транспортная задача
Целью транспортной задачи является минимизация транспортных издержек (или максимизация прибыли) при снабжении грузом нескольких потребителей, если данный груз хранится на удаленных складах.
Постановка задачи.
Пусть требуется развести груз, хранящийся на т складах 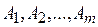 в количествах
в количествах 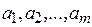 соответственно по n пунктам назначения
соответственно по n пунктам назначения  , подавшим заявки на
, подавшим заявки на 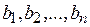 единиц груза. Пусть запас груза на всех складах равен суммарной заявке, то есть:
единиц груза. Пусть запас груза на всех складах равен суммарной заявке, то есть:
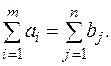
Известно, что стоимость перевозки единицы груза от i-ro склада к j-му потребителю равна 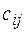 .Требуется составить такой план перевозок, чтобы все заявки были выполнены, а стоимость всех перевозок была минимальна.
.Требуется составить такой план перевозок, чтобы все заявки были выполнены, а стоимость всех перевозок была минимальна.
Аналитическая математическая модель. Пусть  — количество груза, перевозимого со склада
— количество груза, перевозимого со склада 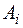 потребителю
потребителю 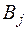 . Прямоугольную матрицу, составленную из величин
. Прямоугольную матрицу, составленную из величин  , будем называть планом перевозок.
, будем называть планом перевозок.
Суммарное количество груза, перевозимое с каждого склада потребителям, должно быть равно запасу на данном складе. То есть:
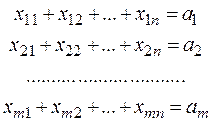
Суммарное количество груза, доставляемое каждому потребителю со складов, должно быть равно заявке данного потребителя:
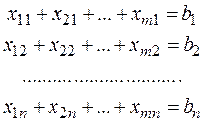
Суммарная стоимость всех перевозок должна быть минимальной
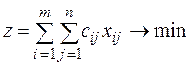
В данной аналитической модели суммарные поставки равны общему количеству заказов. Такие задачи называются сбалансированными.
На практике транспортные задачи оказываются гораздо сложнее. Сумма запасов может превышает сумму заказов (излишек запасов) или, наоборот, сумма запасов может быть меньше, чем сумма заказов (дефицит запасов).
В первом случае часть запасов, очевидно, должна остаться на складах поставщиков, и дополнительный вопрос при этом состоит в том, сколько грузов не вывозить (оставить на складе) у каждого поставщика, чтобы сумма транспортных издержек при выполнении заказов потребителей была бы минимальной. Для определения места, где останутся излишки в таблицы транспортных издержек и в таблицу перевозок добавляется по одному лишнему столбцу. Это трактуется так, как будто появился ещё один, виртуально-фиктивный потребитель, заказ которого равняется разности между суммой всех запасов и суммой всех заказов
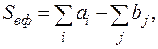
а издержки перевозок грузов к нему от любого поставщика равняются нулю.
Во втором случае, то есть при

предстоит решать, как распределить дефицит между потребителями. Разумеется, в реальности этот случай сложнее для менеджера, отвечающего за доставку заказов потребителям. Решение проблемы будет, по-видимому, определяться приоритетом каждого из потребителей для поставщика или исходом переговоров. Однако если предположить, что все потребители имеют одинаковый рейтинг и проблема состоит только в том, чтобы подешевле развезти весь имеющийся на складах поставщика товар, то этот второй случай с точки зрения оптимизации издержек симметричен первому. Добавим в таблицу транспортных издержек и в таблицу перевозок по одной лишней строке, что можно трактовать, как если бы появился ещё один, виртуально-фиктивный, поставщик. Потребуем, чтобы его запас равнялся разности между суммой всех заказов и суммой всех запасов, а издержки перевозок грузов от него к любому поставщику были равны нулю. Решение конкретных задач ждёт Вас на практических занятиях.
Еще одно возможное осложнение транспортной задачи — это запрещение определенной перевозки от i-го поставщика j-му потребителю для составляемого плана перевозок (ремонт дороги, неплатеж и пр.). В этом случае, естественно, можно было бы просто ввести ограничение  =0. Однако это означает невозможность использования эффективных «транспортных» алгоритмов решения.
=0. Однако это означает невозможность использования эффективных «транспортных» алгоритмов решения.
Чтобы сохранить форму транспортной задачи и учесть этот запрет, достаточно в таблице транспортных издержек заменить стоимость перевозок на очень большое число. Это фактически будет означать, что оптимизационный алгоритм наверняка положит соответствующее значение перевозки  равным нулю, поскольку перевозка по этому маршруту просто крайне невыгодна.
равным нулю, поскольку перевозка по этому маршруту просто крайне невыгодна.
В заключение отметим, что транспортные задачи могут быть сформулированы с учетом и других ограничений. Например, ограничений на неделимость груза, грузоподъемность, аренду и др.
Дата добавления: 2015-10-13; просмотров: 1039;
