Задачи нелинейной оптимизации

На примере модели сбыта продукции рассмотрим зада­чу, в которой целевая функция не является линейной. Такие задачи относятся к задачам нелинейного програм­мирования и также могут быть решены с помощью над­стройки Поиск решения MS Excel.

Постановка задачи.

Предприятие реализует выпускае­мую продукцию, сбыт которой носит сезонный характер. В таблице 21.1 коэффициент сезонности сбыта в каждом квартале указан в строке «Сезонность». Себестои­мость единицы продукции составляет 25 руб., а цена, по которой она реализуется, — 40 руб. В каждом квартале затраты на торговый персонал составляют 8 000 руб., а затраты на рекламу — 10 000 руб. Косвенные затраты составляют 15 % от выручки.

Т а б л и ц а 21.1.

Пусть ожидаемое число продаж 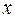зависит от коэффи­циента сезонности k и затрат на рекламу r следующим образом:

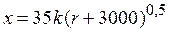
Требуется определить, как влияет распределение за­трат на рекламу на динамику прибыли от продажи про­дукции.

Решение.

Как видно из формулы для числа продаж, первые 5000 р. затраченные на рекламу в первом квартале, приводят к увеличению числа продаж на 1092 единицы, а следующие 5000 р. — только на 775 единиц. То есть зависимость числа продаж от рекламы не является линейной.

Заполним лист MS Excel, как показано на рисунке и исследуем полученную математическую модель.

Вариант 1. Пусть, например, суммарные расходы на рекламу не должны превышать 40 тыс.руб. Требуется оп­ределить расходы на рекламу для получения наибольшей прибыли в первом квартале. Необходимо добиться наи­большей прибыли, изменяя затраты на рекламу в каждом квартале. Используем стандартный прием для поиска ре­шения поставленной задачи со следующими параметрами оптимизации.

Поиск решения даёт результат, при котором прибыль за 1-й квартал увеличивается со значения 14324 руб. до 15093 руб. при увеличении затрат на рекламу в этом квартале на 7093 руб. по сравнению с исходным значением.

Т а б л и ц а 21.2

В заключение отметим, что изложенный материал позволяет проследить технологию исследования простейших оптимизационных моделей в экономике. Более сложные аналитические модели могут быть построены с использованием таких специализированных пакетов, как Mathcad, MS Project и др.

Контрольные вопросы и задачи

21.1. Поясните назначение процедуры аппроксимации.

21.2. Какова последовательность решения задачи аппроксимации?

21.3. Какие инструменты используются в MS Excel для решения уравнений, с помощью которых осуществляется поиск экстремума?

21.4. Сформулируйте общую постановку задачи исследования операций.

21.5. Какие инструменты используются в MS Excel для решения задач оптимизации?

21.6. В чём заключается анализ оптимального решения?

21.7. Сформулируйте понятие о двойственной задаче.

21.8. Что является целью транспортной задачи?

21.9. В чём суть и для чего используется задача о назначениях?