Алгоритм закраски областей, заданных списком вершин
(метод построчного сканирования)
Интерполяция яркости при закраске областей
О линейной интерполяции яркости при закраски области можно говорить, если закрашиваемая фигура плоская т.е. лежит в одной плоскости, например (ХУ).

Рис. 2.9.5.
Плоскость определяется по трём точкам:
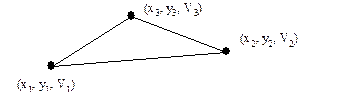
Рис. 2.9.6.
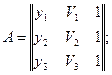
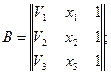
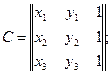
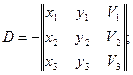
|| || - определитель матрицы;
A·x + B·y + D A В D
V = - ¾¾¾¾¾¾¾ = a·x + b·y + g, где a = - ¾, b = - ¾ , g = - ¾;
C С C C
V = V1 + α (х - х1)+β (у - у1), где
V – яркость в произвольной точке, V1 – яркость известная.
Предварительно производится отсечение многоугольника по полю вывода. Существуют различные задачи закраски: выпуклых многоугольников и многоугольников произвольной формы. Начнем с закраски произвольного многоугольника.

Рис.2.9.7.
Сначала находят ymax и ymin. Далее для текущей у-координаты находят крайнее левое и крайнее правое ребро. Начинают с крайнего левого ребра: идут вправо (и закрашивают соответствующие точки) до пересечения со следующим ребром. Также необходим анализ на наличие локальных экстремумов. В этих точках режим закраски не меняется.
Алгоритм работает с помощью 2-х таблиц:
1. таблица ребер (ТР);
2. таблица активных ребер (ТАР);
В ТР заносятся все ребра, а в ТАР лишь те ребра, которые мы пересекаем.
Составление ТР:
Все ребра делятся на группы по нарастанию у-координаты, а внутри группы рёбра упорядочиваются в соответствии с нарастанием хнач. Ребро в таблицу заносится только 1 раз, горизонтальные ребра игнорируются.
|
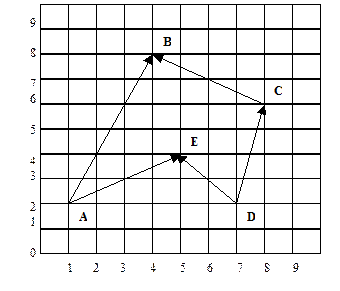
Таблица рёбер:
| Группа, № | Ребро | ymin | ymax | хНАЧ | хКОН | ∆x | VНАЧ | VКОНЕЧ | ∆V |
| АВ | 0.5 | ||||||||
| АЕ | |||||||||
| DC | 0.25 | ||||||||
| DE | -1 | ||||||||
| CB | -2 |
хКОН ¾ хНАЧ VКОНЕЧ ¾ VНАЧ
Dх = ¾¾¾¾¾¾; DV = ¾¾¾¾¾¾¾;
ymax ¾ ymin ymax ¾ ymin
Дата добавления: 2015-09-28; просмотров: 1633;
