Решение одномерных задач методом поиска

Численный метод поиска экстремальных значений функции рассмотрим на примере нахождения минимума функции 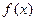на отрезке [а,b]. При этом предполагается, что целевая функция на данном отрезке имеет только один минимум, т.е. унимодальна.

Процесс решения задачи методом поиска состоит в последовательном сужении интервала изменения проектного параметра, называемого интервалом неопределенности. В начале процесса оптимизации его длина составляет 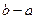. К концу она должна стать меньше заданного допустимого значения ε. Следовательно, оптимальное значение проектного параметра должно находиться в отрезке 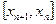, при условии, что .

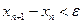Наиболее простым способом сужения интервала неопределенности является деление его на некоторое число равных частей с последующим вычислением значений целевой функции в точках разбиения. Пусть n – число элементарных отрезков, тогда шаг разбиения:

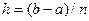
Вычислим значения целевой функции 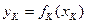в узлах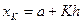 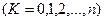. Сравнивая полученные значения 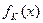, находим среди них наименьшее . Число можно приближенно принять за наименьшее значение целевой функции на отрезке [а,b].

Близость 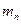к минимуму 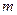зависит от числа точек и для непрерывной функции .

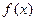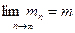
В данном варианте метода поиска, который называется метод перебора, основным недостатком является трудность выбора правильного числа n и погрешности ε. Кроме того, он занимает много времени.

Более экономичным является вариант поиска, использующий унимодальность целевой функции. Для увеличения точности числа 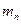не увеличивают число n. Вместо этого сужают интервал неопределенности до размера двух шагов 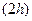. Если не достигается заданная погрешность ε, то его снова разбивают на новое число отрезков и так далее, пока не достигается заданная погрешность.