Решение задачи Коши разностными методами.

Требуется найти функцию 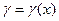, удовлетворяющую уравнению

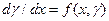(16.1)

и принимающую при 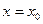заданное значение

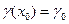. (16.2)

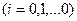Вводится последовательность точек и шаги . В каждой точке 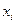, называемой узлом, вместо значений функции 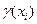вводятся числа 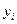, аппроксимирующие точное решение 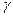на данном множестве точек. Функцию 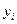, заданную в виде таблицы чисел 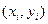называют сеточной.

Далее заменяем значение производной в уравнении (16.1) отношением

конечных разностей. Таким образом, переходим от дифференциальной задачи (16.1), (16.2) относительно функции 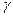к разностной задаче относительно сеточной функции :

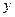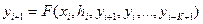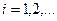, (16.3)

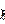(16.4)

Здесь разностное уравнение записано в общем виде. Конкретное выражение его правой части зависит от способа аппроксимации. Для каждого численного метода получается свой вид уравнения (16.3).

Если в правой части уравнения (16.3) отсутствует , то это значит, что явно вычисляется по 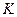предыдущим значениям 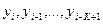. Такая разностная схема называется явной. При этом получается 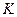- шаговый метод. При 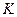=1 метод называется одношаговый, при 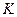=2 – двухшаговый и т.д.

Если в правой части (16.3) имеется , то разностная схема называется неявной и решение уравнения усложняется.

Решение задачи Коши методом Эйлера.

Это простейший численный метод решения задачи Коши.Он основан на разложении искомой функции 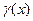в ряд Тейлора в окрестностях узлов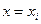 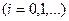, в котором отбрасываются все члены, содержащие производные второго и выше порядков. Это разложение имеет вид:

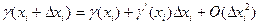, (16.5)

где 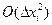- погрешность аппроксимации производной.

Заменяем значение функции 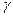в узлах 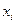значениями сеточной функции 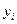, а также, используя уравнение (16.1) получаем

.

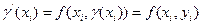Считая узлы сеточной функции равноотстоящими, т.е. 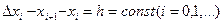, и пренебрегая членами , получаем из равенства (16.5)

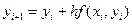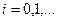, (16.6)

Полагая 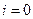из (16.6) находим значение сеточной функци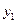и при :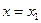

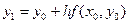. (16.7)

Аналогично могут быть найдены значения сеточной функции в других узлах:

,

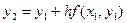……………… (16.8)

.

Построенный алгоритм вычисления (16.7, 16.8) называется методом Эйлера. В нем значение сеточной функции в любом узле вычисляется по ее значению 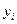в предыдущем узле 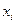. Такие формулы вычисления называются рекуррентными, а метод Эйлера называется одношаговым.