Решение краевой задачи методом конечной разности.

Метод является одной из разновидностей численного метода решения краевой задачи. Он предусматривает переход от решения краевой задачи для

дифференциального уравнения к решению системы алгебраических уравнений относительно искомой функции на заданном множестве точек. Это достигается путем замены производных, входящих в уравнение, их конечно-разностными аппроксимациями.

Рассмотрим сущность данного метода решения на примере ОДУ второго порядка

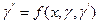, (18.1)

при заданных граничных условиях

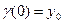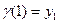; . (18.2)

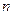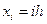
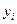Разобьем отрезок [0,1] на равных частей точками . Решение краевой задачи сведем к вычислению значений сеточной функции в узлах . Для этого запишем уравнение (18.1) для внутренних узлов:

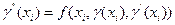, . (18.3)

Заменим производные конечно-разностными аппроксимациями:

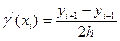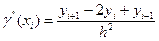, . (18.4)

Подставляя эти выражения (18.4) в уравнение (18.3) получаем систему разностных уравнений

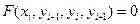; , (18.5)

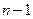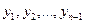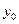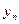которая является системой алгебраических уравнений относительно значений сеточной функции . Входящие в данную систему (при ) и (при 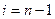) берутся из граничных условий (18.5).