Многомерные задачи оптимизации.

В большинстве реальных задач оптимизации целевая функция зависит от нескольких проектных параметров. Такая задача называется многомерной. Многомерная оптимизация представляет собой поиск наименьшего или наибольшего значения целевой функции

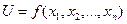, (14.1)

заданной на множестве 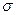, и определение проектных параметров, при которых целевая функция принимает экстремальное значение.

Для решения подобной задачи в области проектирования 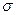, в которой ищется минимум целевой функции (13.1) можно использовать дискретное множество точек (узлов). Интервалы изменения параметров 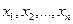разбиваются на части шагами 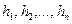. В полученных узлах вычисляется значение целевой функции, и среди них находим наименьшее. Такой метод поиска при многомерной оптимизации требует слишком большого объема вычислений.

Решение многомерной задачи оптимизации методом покоординатного спуска.

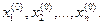Первоначально выбирается некоторая точка с координатами , как показано на рисунке (14.1). Затем фиксируются все координаты функции кроме первой и получаем функцию одной переменной :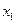

. (14.2)

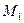
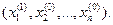Решая таким образом одномерную задачу оптимизации для этой функции, от точки переходим к точке (см. Рис14.1). В ней функция принимает наименьшее значение по координате 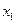или первому проектному параметру при фиксированных остальных координатах. В этом состоит первый шаг процесса оптимизации, заключающийся в спуске по координате .

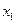Следующий шаг заключается в фиксировании всех координат, кроме второй. Тогда целевая функция будет иметь следующий вид:

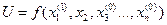. (14.3)

Снова решая задачу одномерной оптимизации, находим наименьшее значение функции при 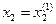, т.е. в точке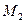 Аналогично производится спуск по координатам 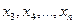. В результате этого получаем последовательность точек 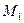, , 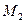…, , 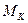в которых значение целевой функции составляет монотонно убывающую последовательность:

(14.4)

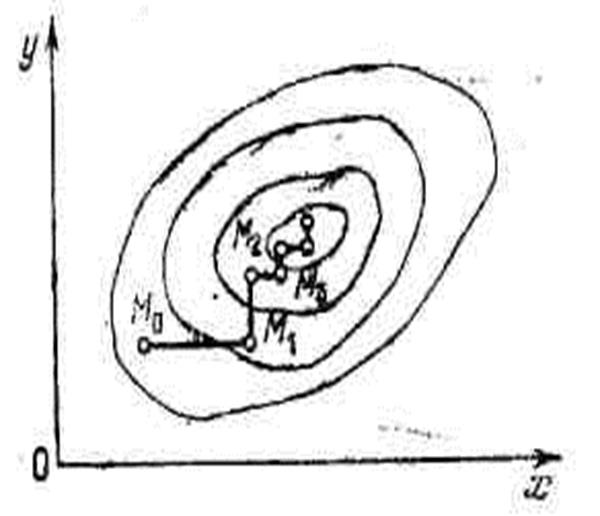
Рисунок 14.1 Пояснение к методу покоординатного спуска.

Таким образом, метод покоординатного спуска сводит задачу многомерной оптимизации к многократному решению одномерной оптимизации по каждому проектному параметру. Сходимость данного метода зависит от вида функции и выбора начального приближения.

Блок-схема метода покоординатного спуска.

Блок-схема данного метода показана на рисунке 14.2. В исходных данных задаются первоначальные значения всех проектных параметров и число этих параметров 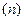. Затем выполняется нахождение целевой функции при исходных значениях всех проектных параметров. После чего определяется минимальное значение функции по одному параметру при фиксации всех остальных. Если не достигается требуемая точность , то вычисления продолжаются.

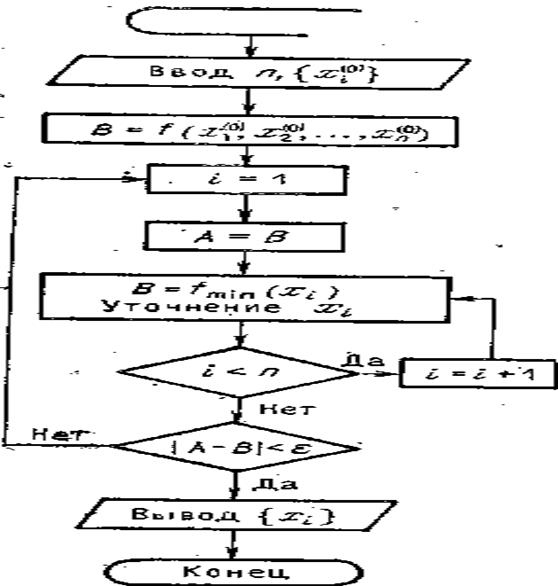
Рисунок 14.2 Блок-схема вычисления методом покоординатного спуска