Типы задач оптимизации.

Выделяют два типа задач оптимизации – безусловные и условные. Безусловная задача состоит в отыскании максимума или минимума целевой функции (1) от n переменных и определении соответствующих значений аргументов на некотором множестве 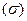n-мерного пространства.

Условные задачи оптимизации или задачи с ограничениями – такие, при формулировке которых задаются некоторые условия (ограничения) на множестве 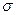. Эти ограничения задаются совокупностью некоторых функций, удовлетворяющих уравнениям или неравенствам.

Ограничения-равенства выражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения. Эти ограничения отражают законы природы, наличие ресурсов и т.п. Ограничения уменьшают область проектирования в соответствии с физической сущностью задачи. Аналогично могут вводиться ограничения-неравенства.

Одномерная оптимизация.

Одномерная задача оптимизации формулируется как поиск наименьшего или наибольшего значения целевой функции 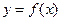, заданной на множестве 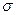, и определение значения проектного параметра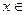 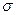, при котором целевая функция принимает экстремальное значение. Функция 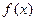может достигать своего минимального или максимального значения либо на граничных точках отрезка [а,b], либо в точках минимума или максимума.

Производная 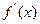в экстремальных точках всегда обращается в нуль. Это необходимое условие экстремума. Следовательно, для определения наименьшего или наибольшего значения функции 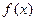на отрезке [а,b] надо вычислить ее значения во всех критических точках и на границах отрезка, а затем сравнить полученные значения. Наименьшее или наибольшее из них и будет искомым значением. А значения параметра, при которых получено экстремальное значение функции, будет оптимальным.