Примеры. 1)
Применим метод Острограденного, т. к. Q(x) содержит множитель (x2 + 1)2.
Q(x) = (x + 1)(x2 + 1)2 /m = 5/
Q1(x) = (x + 1)(x2 + 1) /m1 = 3/тогда P1(x) = cx2 + dx + k
Q2(x) = x2 + 1 /m2 = 2/ P2(x) = ax + b
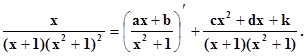
Запишем (7):
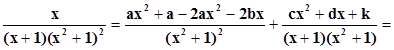
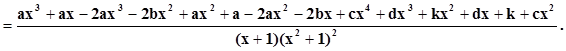 |
или
Данная и полученная дроби тождественно равны и имеют одинаковые знаменатели, поэтому их числители должны быть тоже тождественно равны. Но тогда коэффициенты при соответствующих степенях тоже равны:
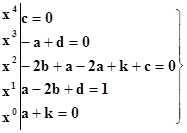
получаем: a = ¼, b = – ¼, c = 0, d = ¼, k = – ¼.
Тогда по (6)имеем
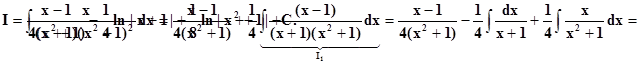
I1вычисляем как раньше:
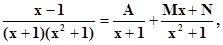
отсюда Ax2 + A + Mx2 + Nx + Mx + N ≡ x – 1и
A = – 1, M = 1, N = 0
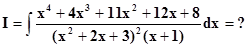
2) Вычислить
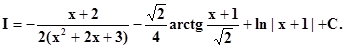
Ответ:
§6 Интегрирование некоторых иррациональных функций.
Функция f(x) называется иррациональной, если она получена с помощью четырёх рациональных операций (сложения, вычитания, умножения, деления) и возведения в рациональную степень (не целую) переменной интегрирования или некоторого рационального выражения от этой переменной.
Далеко не всегда можно выразить интеграл от иррациональной функции с помощью элементарных функций (интеграл “не берётся” в конечном виде).
Мы рассмотрим некоторые наиболее употребительные иррациональные выражения, неопределённые интегралы от которых могут быть выражены через элементарные функции.
1) Интегрирование выражений R(x,xm/n,…,xr/s), где m/n,...,r/s рациональные дроби. Здесь символ R(x,xm/n,…,xr/s) означает, что над x,xm/n,…,xr/s производятся только рациональные действия (четыре перечисленных выше и возведение в натуральную степень). /“R”=”рациональное выражение от...”/. Пусть k– наименьший общий знаменатель дробей m/n,...,r/s. Осуществим замену X = tk , тогдаdx = ktk-1dt.
Каждая дробная степень Xтогда выразится через натуральную степень t и потому
подинтегральное выражение станет рациональной функцией от t. В этой связи замену X = tk называют рационализирующей подстановкой.
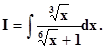
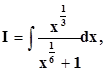
 Пример. Вычислить неопределённый интеграл
Пример. Вычислить неопределённый интеграл
Решение.Т. к. то наименьший общий знаменатель дробей 1/3и 1/6
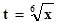
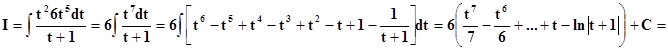
будет 6.Потому берём x = t6 ,откуда dx = 6t5dtи . Тогда
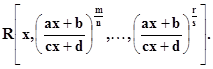
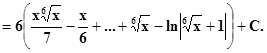 |
Дата добавления: 2015-10-05; просмотров: 750;
