Примеры.

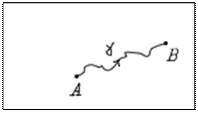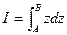(1) , где интеграл берётся по любой спрямляемой кривой, соединяющей точки А и В. Посчитаем, исходя из определения. Если кривая спрямляема, то предел существует. Интегральные суммы: 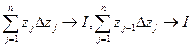знаем, что сходятся к I.

Возьмём среднее арифметическое: .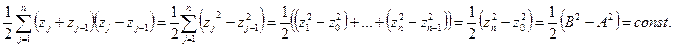

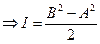(2) Вычислим интеграл: 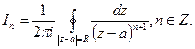Это гладкая кривая, следовательно введём параметризацию и тогда посчитаем. Уравнение окружности (параметризуемое): 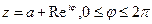. 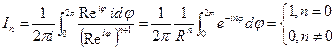т.к. это интеграл от sin, cos по периоду.

ИНТЕГРАЛЬНАЯ ТЕОРЕМА КОШИ

Замечание. Если 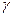замкнутая и спрямляемая кривая, то .

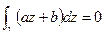Почему? Т.к. 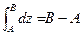и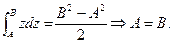

Гипотеза: Поскольку равенство 0 верно для линейной функции (по замкнутой кривой), тогда верно для любой голоморфной функции.