Остроградского, который позволяет заменить вычисление интеграла
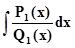
вычислением интеграла , где разложение Q1(x)содержит квадратичные
множители (и линейные тоже!) только в первых степенях. Поступают так:
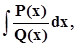
Пусть имеем где Q(x) = (x – a)a … (x – b)β(x2 + px + q)μ … (x2 + lx + s)ν.
Представим Q(x)в виде произведения двух множителей
Q(x) = Q1(x) ∙ Q2(x),
причём Q1(x)есть произведение всех разных множителей из Q(x)взятых по одному разу
Q1(x) = (x – a) … (x – b)(x2 + px + q) … (x2 + lx + s),
а Q2(x)есть произведение оставшихся неиспользованными сомножителей из Q(x)
Q2(x) = (x – a)a – 1 … (x – b)β – 1(x2 + px + q)μ – 1 … (x2 + lx + s)ν – 1.
Остроградский (известный русский учёный) доказал следующую формулу:
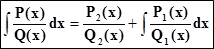
(6)
ЗдесьQ(x), Q1(x), Q2(x),известные многочлены, степени которых есть соответственно m, m1, m2. P(x)тоже известный многочлен степени ≤ m – 1. P1(x)иP2(x)есть пока ещё неизвестные многочлены степеней соответственно не выше m1 – 1и m2 – 1 /все дроби правильные/:
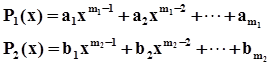
/a1, a2, … b1, b2, … –неизвестные пока (буквенные) коэффициенты /.
Для нахождения этих коэффициентов продифференцируем равенство (6):
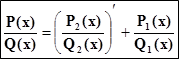
(7)
По методу неопределённых коэффициентов мы найдём из (7)коэффициенты, а, значит, и многочлены P1(x)и P2(x). Подставим их в (6)и 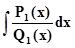останется только вычислить
,
где Q1(x)в своём разложении содержит разные множители только в первых степенях.
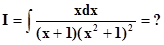
Дата добавления: 2015-10-05; просмотров: 523;