Справедлива (доказательство опускаем) следующая
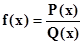
ТеоремаВсякая правильная несократимая рациональная дробь может
быть представлена как сумма конечного числа простейших рациональных дробей, а именно
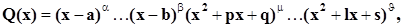 если (2)
если (2)
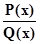
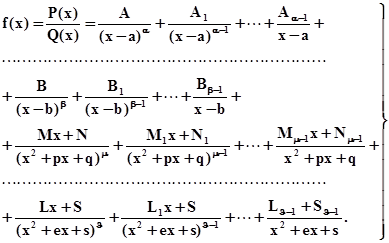 то дробь может быть представлена в виде:
то дробь может быть представлена в виде:
(3)
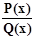 На практике эту теорему применяют следующим образом. Каким – либо образом знаменатель дроби Q(x) представляют в виде (2), причём квадратные трёхчлены имеют дискриминанты отрицательные и потому уже не могут разлагатся в произведение линейных множителей с действительными коэффициентами. Затем пишут для дроби
На практике эту теорему применяют следующим образом. Каким – либо образом знаменатель дроби Q(x) представляют в виде (2), причём квадратные трёхчлены имеют дискриминанты отрицательные и потому уже не могут разлагатся в произведение линейных множителей с действительными коэффициентами. Затем пишут для дроби
соответствующее разложение (3) с буквенными коэффициентами A,A1, … Ln-1,
Sn-1. Эти коэффициенты определяют по методу неопределённых коэффициентов.Равенство (3) есть тождество, поэтому, приведя дроби справа к наименьшему общему знаменателю (он, очевидно будет равен Q(x)), получают тождественное равенство числителей, двух многочленов – P(x)и того, который получится справа. Приравнивая коэффициенты при одинаковых степенях x,получают систему линейных уравнений относительноA, A1, A2, … Ln-1, Sn-1,из которой их и определяют.
Замечание 1.Уравнение для определения коэффициентов можно получать и другим способом. Т. к. полученное равенство числителей есть тождество, то давая xконкретные (удобные!) значения, имеют необходимые уравнения для определения этих коэффициентов (более простые, чем в описанной выше системе).
Замечание 2. Из выше изложенного следует такой вывод: неопределённый интеграл от рациональной функции всегда может быть выражен через конечное число элементарных функций.
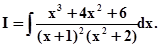 Примеры 1)Вычислить интеграл
Примеры 1)Вычислить интеграл
Подинтегральная функция f(x) является правильной рациональной дробью. Знаменатель уже разложен в произведение простых (неприводимых) множителей, т. к. x2 + 2не имеет действительных корней /x1,2 = ± i Ö2/.
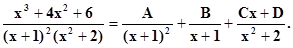 |
Разложим подинтегральную дробь в сумму простейших дробей:
Приведём дроби справа к наименьшему общему знаменателю и приравняем числители:
x3 + 4x2 + 6 º A(x2 + 2) + B(x +1)(x2 + 2) + (Cx + D)(x +1)2. (4)
или x3 + 4x2 + 6 = (B + C)x3 + (A + B + 2C +D)x2 + (2B + 2D + C)x + (2A + 2B + D).
Приравнивая коэффициенты при x3, x2, x1, x0,получим систему четырёх линейных уравнений с четырмя неизвестными A, B, C, D:
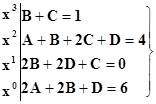
(5)
Ещё из тождества (4) при удобном значении x = – 1получаем дополнительное простое уравнение: 3A = 9, откуда A = 3
Последующее решение системы (5) даст: B = 1/3, C =2/3, D = –2/3
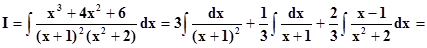
Итак,
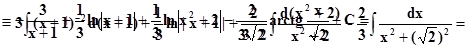 |
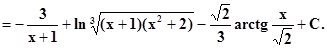 |
2)Вычислить самостоятельно
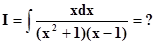
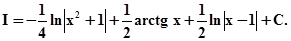
Ответ:
Дата добавления: 2015-10-05; просмотров: 795;
