Интегрируя почленно это равенство, получим
uδ =òudδ + òδdu.
или òudδ = uδ – òδdu. (2).
Формулу (2) и называют формулой интегрирования по частям.Она заменяет вычисление данного интеграла òudδвычислениемòδdu (uδ –это уже часть ответа) и её применение оправдано, если этот новый интеграл вычисляется проще. Разбиение подинтегрального выражения в данном интеграле на два множителя uи dδзависит от вида этого выражения и определённого навыка, приобретаемого через решение достаточного количества примеров (dx, конечно, всегда входит в dδ). Рассмотрим некоторые особенности применения формулы (2) на конкретных примерах.
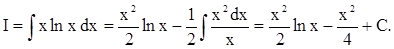
1) I =òx ln x dx = ?Итак
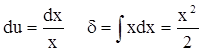 Положим u = ln x dδ = xdx
Положим u = ln x dδ = xdx
Замечание.Когда мы определяем δ по dδ, можно брать С = 0, т. к. дальнейшие вычисления будут проще, а окончательный результат (значение I) не пострадает, потому что произвольная постоянная С появится там вместе с вычислением δdu.
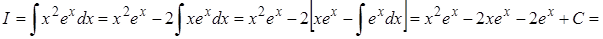
2).
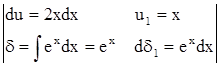 u = x2 du1 = dx
u = x2 du1 = dx
dδ = exdx δ1 = ex =ex(x2 – 2x–1) + C.
Как мы видим, в одном примере можно применять формулу (2) несколько раз.
Метод интегрирования по частям применяется часто. Именно по частям вычисляются неопределённые интегралы вида:
òxksin(ax)dx, òxkcosaxdx, òxkeaxdx, òxkabxdx, /u=xk,нужно прим. ф-лу (2) k раз/.
òxkln(ax)dx, òxkarcsin x dx, òxkarccos xdx, òxkarctg x dx, òxkarcctg x dx
/u = ln axилиu = arcsin x,…/
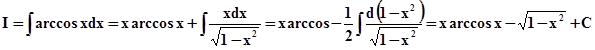
3)
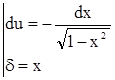
u = arccos x
dδ = dx
4). I = òexsin x dx = – excos x + òexcos x dx = – excosx +[exsin x – òexsin x dx]=
= ex(sin x – cos x) – I


u = ex du = exdx u1 = ex du1 = exdx
dδ = sin x dx δ = – cos x dδ1 = cos x dx δ1 = sin x
Выражая Iиз полученного (подчёркнутого) равенства, мы окончательно получим:
2 I = ex(sin x – cos x) и I = ½ ex(sin x – cos x)
Возникшую после двухкратного применения формулы (2) ситуацию обычно называют приведением интеграла к самому себе.
5).Самостоятельно вычислить неопределённые интегралы.
а) I = òx arctg x dx Ответ: I = ½[(x2 +1)arctg – x] + C.
б) I = ò(x2 + 7x – 5)cos 2x dx
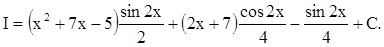
Ответ:
/Указание: u = x2 + 7x – 5/
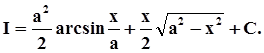
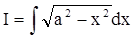
c) Ответ:
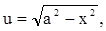
/Указание: дважды/.
§4. Некоторые общие замечания об интегрировании функций.
Мы уже отмечали (пока без доказательства), что всякая непрерывная функция является интегрируемой, т. е. Неопределённый интеграл òf(x)dx = F(x) + Cсуществует. Однако, далеко не всегда первообразная F(x) может быть выражена некоторой элементарной функцией. Часто в таких случаях говорят, что неопределённый интеграл “не берётся в конечном виде”. Примерами “неберущихся” интегралов могут служить
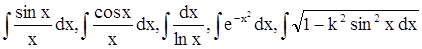
,òsin(x2)dx, òcos(x2)dx.
и многие другие. Эти первообразные функции существуют, но, не являясь элементарными функциями, очевидно представляют функции иной природы. Некоторые из этих неэлементарных функций часто используются на практике и хорошо изучены, табулированы. Некоторые даже получили специальные обозначения и названия:
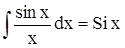
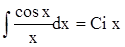
– интегральный синус, – интегральный косинус,
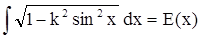
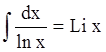
– интегральный логарифм, –
эллиптический интеграл.
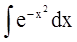
С помощью первообразной Лаплас определил “свою” функцию
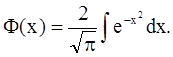
/функцию Лапласа/
Она имеет широкие применения в теории вероятностей. Можно утверждать, что большинство первообразных не выражаются через конечное число операций над элементарными функциями (не берутся в конечном виде).
Поэтому очень важно определить и изучить те классы функций, первообразные от которых являются элементарными функциями (берутся в конечном виде).Наиболее простым и важным таким классом являются рациональные функции.
§5. Интегрирование рациональных функций.
Рациональной функцией называется функция, являющаяся отношением двух многочленов (полиномов):
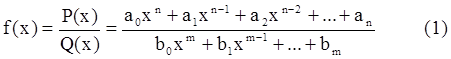
Если Q(x) ≡ 1, то f(x) = P(x) , т.е. многочлен является частным случаем рациональной функции – целая рациональная функция.Рациональную функцию (1) /Q(x)≢1/ называют дробно-рациональной функцией(или рациональной дробью).
Без ограничения общности можно считать, что многочлены P(x) и Q(x) не имеют одинаковых нулей (корней), т. к. в противном случае можно сократить дробь (1) на общие множители.
Рациональною дробь (1) называют правильной, если степень числителя ниже степени знаменателя, т. е. n < m. Если же n ≥ m, (1) называется неправильной.
Если рациональная дробь (1) неправильная, то её можно всегда представить в виде суммы целой рациональной функции (целой части) и правильной рациональной дроби. /например, деля числитель на знаменатель как два полинома/:
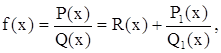 |
где R(x) – полином, P1(x)/Q1(x) – правильная дробь.
Интегрирование полинома не составляет труда, поэтому будем рассматривать
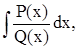
полагая P(x)/Q(x)правильной.
1.Изучим сначала интегрирование простейших (элементарных) рациональных дробей.
Определение.Правильные рациональные дроби вида
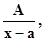
I.
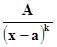
II. /k –натуральное число ≥ 2/,
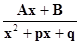
III. /знаменатель не имеет действительных корней, т. е.
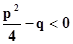
; A, B, a, p, q –действительные числа /,
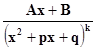
IV. /k –натуральное число ≥ 2;знаменатель не имеет действительных корней/,
называются соответсвенно простейшими рациональными дробями I, II, III и IVтипов.
Интегрирование дробей первых трёх типов осуществляется просто.
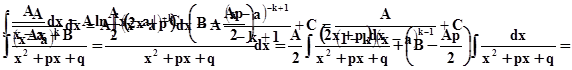 |
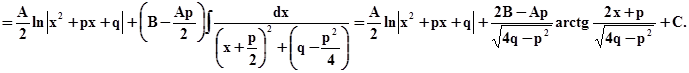
/см. §3/.
Интегрирование простейших дробей IV типа осуществляется таким же методом, но выкладки значительно сложнее. Мы в этом же параграфе рассмотрим метод Остроградского, который позволит интегрировать любые рациональные дроби, применяя интегралы только от простейших дробей первых трёх типов.
Дата добавления: 2015-10-05; просмотров: 819;
