Интегрирование биноминальных дифференциалов.
Биноминальным дифференциалом называется выражение вида xm(a + bxn)pdx,где a, b –дествительные числа;m, n, p – рациональные.
В 1853 году П. Л. Чебышевым (знаменитым русским математиком) была установлена теорема о том, что интеграл вида xm(a + bxn)pdxберётся в конечном виде лишь в следующих трёх случаях: a) когда p –целое число,
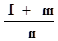
б) когда – целое число,
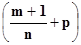
с) когда – целое число.
Во всех остальных случаях этот интеграл в конечном виде не берётся. Доказательство теоремы сложное, использует сложный аналитический аппарат, поэтому его не приводим. Покажем только, как же вычислить интеграл в тех трёх случаях, когда он берётся в конечном виде.
а) p– целое число (положительное, отрицательное или 0).
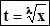 Обозначим через λ –общий знаменаталь чиселmиn.Тогда подинтегральное выражение xm(a + bxn)p = R(λ√x)и потому рационализирующей подстановкой будет
Обозначим через λ –общий знаменаталь чиселmиn.Тогда подинтегральное выражение xm(a + bxn)p = R(λ√x)и потому рационализирующей подстановкой будет
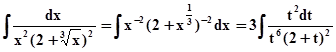 Тогда x = t λ, dx = λt λ –1dt. òxm(a + bxn)pdx = òt λm(a + bxλn) λt λ –1dt.
Тогда x = t λ, dx = λt λ –1dt. òxm(a + bxn)pdx = òt λm(a + bxλn) λt λ –1dt.
Пример.– интеграл от
рациональной функции по t. (m = – 2, n = 1/3, p = – 2 –целое, λ = 3)
t = 3√x, x = t3, dx = 3t2dt, x -2 = t -6, 2 + x1/3 = 2 + t. /закончить самостоятельно/.
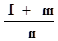 б) –целое (p –дробное: p = r/s).Рационализирующей подстановкой
б) –целое (p –дробное: p = r/s).Рационализирующей подстановкой
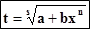
является в этом случае .
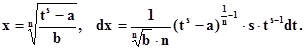
Тогда a + bxn = ts,
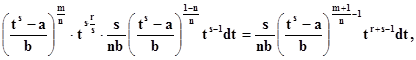
Получим xm(a + bxn)pdx =
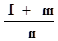
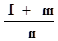
т. к. – целое число, то –1 –тоже целое. Пришли к случаю а),а
потому выражение действительно рационализируется.
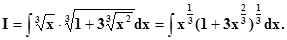
Дата добавления: 2015-10-05; просмотров: 781;
