Вычисление вероятности для функции от ДСВ и вывод ее распределения
Функцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина X примет значение, меньшее х, то есть 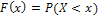 .
.
Функция распределения обладает следующими свойствами:
1. Значения функции распределения принадлежат отрезку [0;l]: 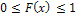 .
.
2. Функция распределения есть неубывающая функция: 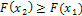 , если
, если 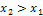 .
.
Следствие 1: Вероятность того, что случайная величина примет значение, заключенное в интервале 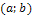 , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале: 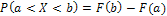 .
.
Следствие 2: Вероятность того, что непрерывная случайная величина X примет одно определенное значение, например 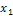 , равна нулю:
, равна нулю: 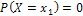 .
.
3. Если все возможные значения случайной величины X принадлежат интервалу 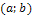 , то F(x) = 0 при
, то F(x) = 0 при 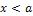 ; F(x) = 1 при
; F(x) = 1 при 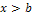 . Теоретические исследования показали, что в большом числе встречающихся на практике случаев с достаточным основанием можно считать, что случайные величины распределены по нормальному закону. Дифференциальная функция нормального распределения:
. Теоретические исследования показали, что в большом числе встречающихся на практике случаев с достаточным основанием можно считать, что случайные величины распределены по нормальному закону. Дифференциальная функция нормального распределения:
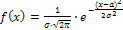 ,
,
где 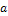 - математическое ожидание;
- математическое ожидание; 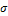 - среднее квадратическое отклонение случайной величины X.
- среднее квадратическое отклонение случайной величины X.
Вероятность попадания нормально распределенной случайной величины Х в интервал 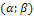 находят по формуле
находят по формуле
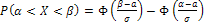 .
.
Вероятность того, что абсолютная величина отклонения « 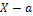 » меньше
» меньше 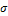 , равна:
, равна: 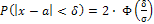 .
.
Дата добавления: 2015-09-25; просмотров: 1668;
