Основные законы распределения ДСВ

Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т.е. между двумя соседними возможными значениями нет возможных значений), которые эта величина принимает с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть задан в виде таблице, первая строка которой содержит возможные значения а вторая - вероятности .

где .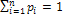

Если множество возможных значений X бесконечно, то ряд сходится и его сумма равна единице.

Закон распределения дискретной случайной величины можно изобразить графически, для чего в прямоугольной системе координат строят точки , ,…, , (где , - возможные значения X, -соответствующие вероятности) и соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.

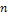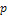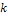Биноминальным называют закон распределения дискретной случайной величины X - числа появлений события в независимых испытаниях, в каждом из которых вероятность появления события равна ; вероятность возможного значения (числа появлений события) вычисляют по формуле Бернулли:

Если число испытаний велико, а вероятность 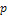появления события в каждом испытании очень мала, то используют приближенную формулу

где 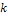- число появлений события в 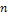независимых испытаниях, (среднее число появлений события в 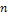испытаниях), и говорят, что случайная величина распределена по закону Пуассона.