Примеры. Задача 1. Случайная величина Х задана функцией распределения
Задача 1. Случайная величина Х задана функцией распределения
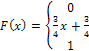
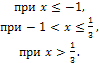
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале 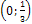 .
.
Решение: Вероятность того, что случайная величина примет значение, заключенное в интервале (a;b), равна приращению функции распределения на этом интервале: 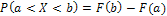 .
.
Положив 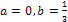 , получим
, получим
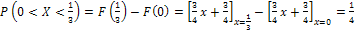 .
.
Задача 2. Заданы математическое ожидание 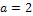 и среднее квадратическое отклонение
и среднее квадратическое отклонение  нормально распределенной случайной величины X. Требуется найти:
нормально распределенной случайной величины X. Требуется найти:
а) вероятность того, что X примет значения, принадлежащие интервалу (1; 4);
б) вероятность того, что абсолютная величина отклонения «X -а» окажется меньше 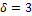 .
.
Решение: а) воспользуемся формулой 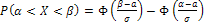 .
.
По условию задачи 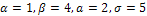 . Следовательно,
. Следовательно,
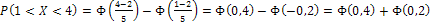 .
.
По таблице приложения 2: 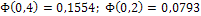 .
.
Искомая вероятность попадания нормально распределенной случайной величины в интервал (1;4) равна:
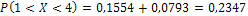 .
.
б) вероятность того, что абсолютная величина отклонения «Х-а» меньше 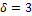 , равна
, равна 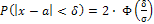 ;
;
 .
.
Ответ: а) 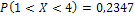 ;
;
б) 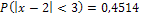 .
.
Дата добавления: 2015-09-25; просмотров: 6078;
