Неопределенный интеграл и методы его вычисления
- Первообразная функция и неопределённый интеграл
Основные свойства неопределённого интеграла и правила интегрирования
Для решения задачи нахождения по заданной производной 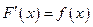 самой функции
самой функции 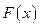 служит операция интегрирования функций, являющаяся обратной по отношению к операции дифференцирования.
служит операция интегрирования функций, являющаяся обратной по отношению к операции дифференцирования.
Дифференцируемая на некотором промежутке 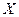 функция
функция 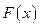 называется первообразной для функции
называется первообразной для функции 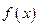 , определенной на том же промежутке, если для каждого числа
, определенной на том же промежутке, если для каждого числа 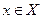 выполняется равенство:
выполняется равенство:
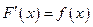 . (1.1)
. (1.1)
Теорема. Если функция 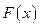 является первообразной для функции
является первообразной для функции 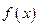 на множестве
на множестве 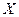 , то совокупность всех первообразных для
, то совокупность всех первообразных для 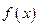 на этом множестве состоит из функций
на этом множестве состоит из функций 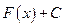 , где С - произвольная постоянная.
, где С - произвольная постоянная.
Доказательство. 1) Так как
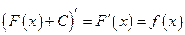 , (1.2)
, (1.2)
то при любом выборе постоянной С функция 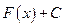 является первообразной для
является первообразной для 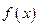 .
.
2) Пусть 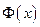 - произвольная первообразная для функции
- произвольная первообразная для функции 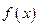 , т.е.
, т.е.
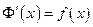 ,
, 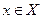 . (1.3)
. (1.3)
Рассмотрим функцию
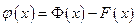 . (1.4)
. (1.4)
Имеем:
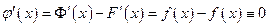
на множестве Х. В силу теоремы Лагранжа о конечных приращениях функция 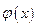 является постоянной:
является постоянной: 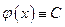 . Следовательно,
. Следовательно,
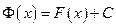 . (1.5)
. (1.5)
Неопределенным интегралом от непрерывной функции 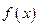 , заданной на Х, называется множество всех первообразных для функции
, заданной на Х, называется множество всех первообразных для функции 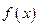 , определенных на этом множестве Х.
, определенных на этом множестве Х.
Обозначается: 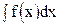 . Читается: «интеграл
. Читается: «интеграл 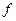 от икс дэ икс». По определению
от икс дэ икс». По определению
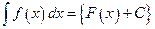 ,
, 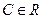 . (1.6)
. (1.6)
Обычно фигурные скобки в правой части опускают и записывают (1.6) в виде:
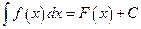 , (1.7)
, (1.7)
считая С произвольной постоянной.
Функция 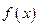 называется подынтегральной функцией, а дифференциал
называется подынтегральной функцией, а дифференциал
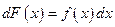 (1.8)
(1.8)
- подынтегральным выражением. Знак 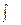 называется знаком неопределенного интеграла, а переменная
называется знаком неопределенного интеграла, а переменная 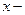 переменной интегрирования.
переменной интегрирования.
Из (1.7) непосредственно следует:
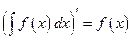 ,
, 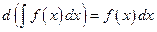 ,
, 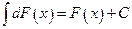 . (1.9)
. (1.9)
Теорема. Справедливы следующие правила интегрирования функций:
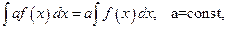 (1.10)
(1.10)
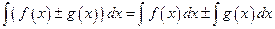 , (1.11)
, (1.11)
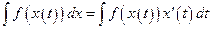 , (1.12)
, (1.12)
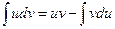 . (1.13)
. (1.13)
Доказательство. Дифференцируя левые и правые части этих равенств с учетом формул (1.9), приходим к одинаковому результату. Действительно,
1) 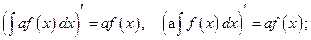
2) 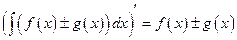 ,
, 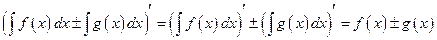 ;
;
3) 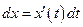 ,
, 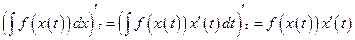 ;
;
4) 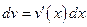 ,
, 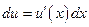 ,
, 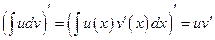 ,
,
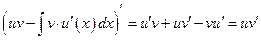 .
.
Правило (1.12) называется правилом «замены переменных», правило (1.13) называется правилом «интегрирования по частям».
Таблица основных формул интегрирования
Таблица неопределенных интегралов
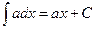
| 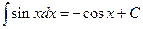
|
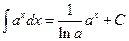
| 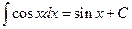
|
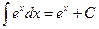
| 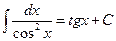
|
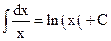
| 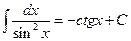
|
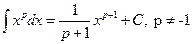
| 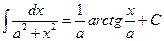
|
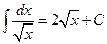
| 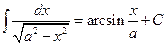
|
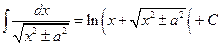
| 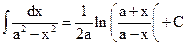
|
Для доказательства правильности формул таблицы достаточно продифференцировать обе её части с использованием свойств неопределённого интеграла и формул дифференцирования и убедится в совпадении результатов.
Рассмотрим несколько примеров.
№1. 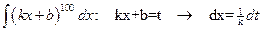
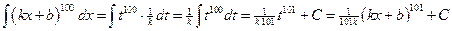 .
.
№2. 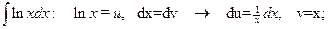
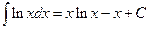 .
.
№3. 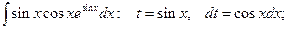
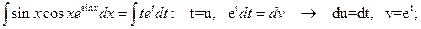
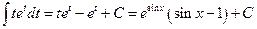 .
.
№4. 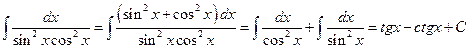 .
.
№5. 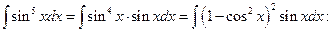
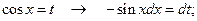
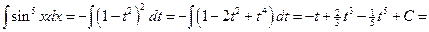
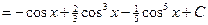 .
.
№6. 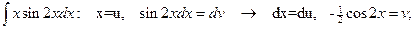
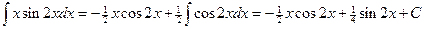 .
.
№7. 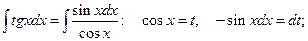
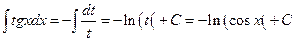 .
.
№8. 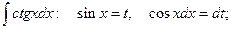
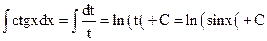 .
.
№9. 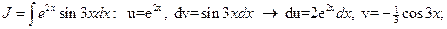
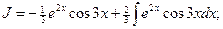
Вычисляем
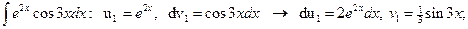
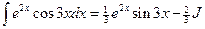 .
.
Получаем:
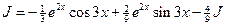 .
.
Следовательно,
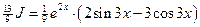 , т.е.
, т.е. 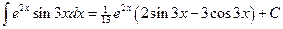 .
.
№10. 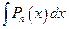 , где
, где 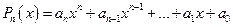 - многочлен степени
- многочлен степени 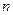 с действительными коэффициентами
с действительными коэффициентами 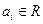
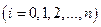 . Используя правила (1.10), (1.11) и таблицу (1.14), находим:
. Используя правила (1.10), (1.11) и таблицу (1.14), находим:
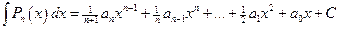 . (2.1)
. (2.1)
Дата добавления: 2015-09-29; просмотров: 920;
