Способы интегрирования некоторых других классов функций
Интегралы вида
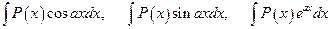 , (4.1)
, (4.1)
где 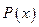 - многочлен, берутся по частям, причем за u берется
- многочлен, берутся по частям, причем за u берется 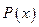 . Интегрировать по частям нужно столько раз, какова степень многочлена
. Интегрировать по частям нужно столько раз, какова степень многочлена 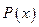 .
.
Пример. 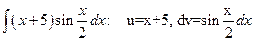
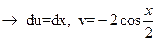 ;
;
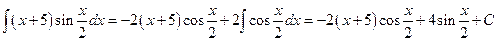 .
.
Интеграл вида
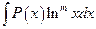 , (4.2)
, (4.2)
где 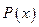 - многочлен, берется по частям. При этом за
- многочлен, берется по частям. При этом за 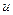 берется
берется 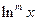 .
.
Пример. 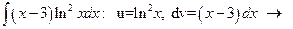
 ;
;
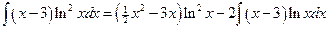 .
.
Вычисляем 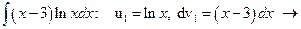
 ;
;
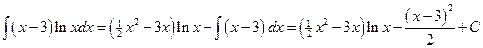 .
.
Следовательно,
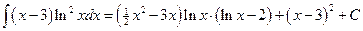 .
.
Пусть 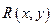 - рациональная функция переменных х и у. Интегралы вида
- рациональная функция переменных х и у. Интегралы вида
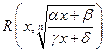 (4.3)
(4.3)
сводятся к интегралам от рациональных функций подстановкой
 . (4.4)
. (4.4)
Действительно, из (4.4) находим:
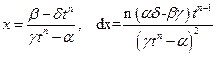 . 4.5)
. 4.5)
Пример. 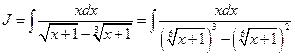 .
.
Обозначим 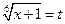
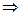
 ,
, 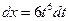 . Следовательно,
. Следовательно,
 =
=
= 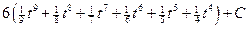 =
=
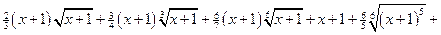
 .
.
Выражение
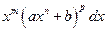 , (4.6)
, (4.6)
где 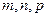 - рациональные числа, называется биномиальным дифференциалом. Их интегрирование сводится к интегрированию дробно-рациональных функций только в трех случаях:
- рациональные числа, называется биномиальным дифференциалом. Их интегрирование сводится к интегрированию дробно-рациональных функций только в трех случаях:
1) 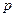 - целое, подстановка
- целое, подстановка 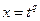 , где
, где 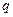 - общий знаменатель дробей m и n;
- общий знаменатель дробей m и n;
2) 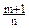 - целое, подстановка
- целое, подстановка  , где
, где 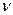 - знаменатель числа р;
- знаменатель числа р;
3) 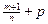 - целое, подстановка
- целое, подстановка  .
.
Выдающийся русский математик П.Л. Чебышёв доказал, что только в этих трех случаях интегралы от биномиальных дифференциалов (4.6) выражаются через элементарные функции.
Примеры. №1. 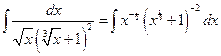 .Здесь
.Здесь 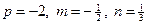 , т.е. имеем 1ый случай (р - целое). Положим:
, т.е. имеем 1ый случай (р - целое). Положим: 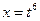
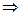
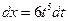 ,
,
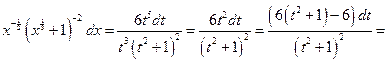
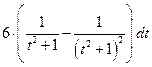 .
.
Следовательно,
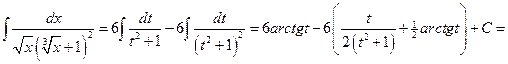
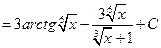 .
.
№2. 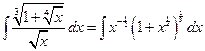 .
.
Здесь 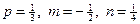 , т.е.
, т.е. 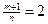 - целое. Имеем 2ой случай. Полагаем
- целое. Имеем 2ой случай. Полагаем 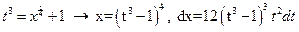 . Следовательно,
. Следовательно,
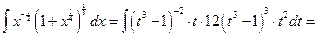
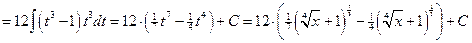
№3. 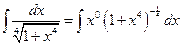 .
.
Здесь 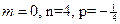 . Имеем 3й случай. Положим
. Имеем 3й случай. Положим 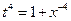
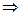
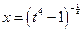 ,
, 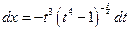 ,
, 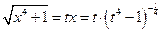 . Следовательно,
. Следовательно,
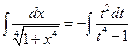 .
.
Имеем:
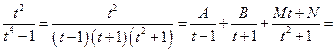
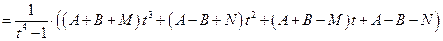 ,
,
т.е.
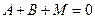 ,
,  ,
, 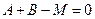 ,
, 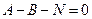 ®
®
® 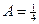 ,
,  ,
, 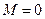 ,
, 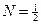 .
.
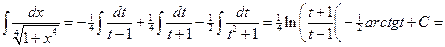
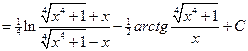 .
.
Интегралы вида
 ,
, 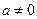 (4.7)
(4.7)
сводятся к интегралам от дробно-рациональных функций одной из трех подстановок Эйлера:
1) 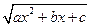 =
= 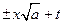 , если
, если 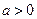 ; (4.8)
; (4.8)
2) 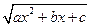 =
= 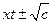 , если
, если  ; (4.9)
; (4.9)
3) 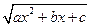 =
= 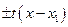 или
или 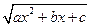 =
= 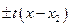 , (4.10)
, (4.10)
если 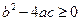 , а
, а 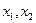 - корни квадратного трехчлена.
- корни квадратного трехчлена.
Примеры. №1. 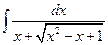 .(
.( 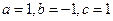 , 1ая или 2ая подстановки). Положим
, 1ая или 2ая подстановки). Положим 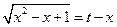 ®
® 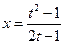 ,
,  ,
,  . Имеем
. Имеем
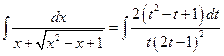 ;
;
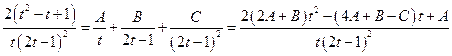 .
.
Следовательно, 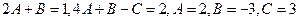 .
.
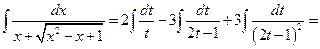
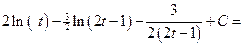
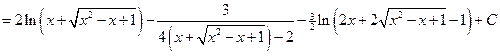 .
.
№2. 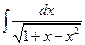 .(
.( 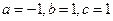 , 2я или 3я подстановки). Положим
, 2я или 3я подстановки). Положим 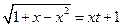 ®
® 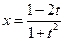 ,
, 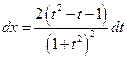 ,
,  . Следовательно,
. Следовательно,
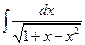 =
= 
 .
.
№3. 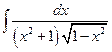 .(
.( 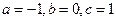 , 2я или 3я подстановки). Положим
, 2я или 3я подстановки). Положим 
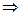
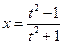 ,
,  ,
, 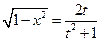 ,
, 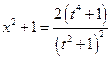 ,
, 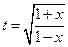 . Следовательно,
. Следовательно,
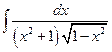 =
= 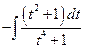 .
.
Имеем:
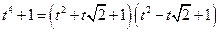 ;
;
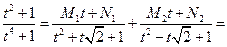

т.е. 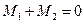 ,
, 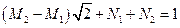 ,
, 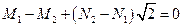 ,
,  .
.
Следовательно, 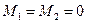 ,
, 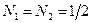 . Значит,
. Значит,
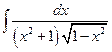 =
= 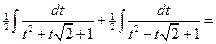

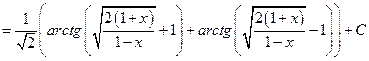 .
.
Интегралы вида
 , (4.11)
, (4.11)
где 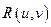 - рациональная функция двух переменных, сводятся к интегрированию дробно-рациональных функций универсальной подстановкой
- рациональная функция двух переменных, сводятся к интегрированию дробно-рациональных функций универсальной подстановкой
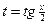 . (4.12)
. (4.12)
Действительно,
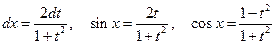 . (4.13)
. (4.13)
Пример. 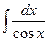 . Положим:
. Положим: 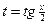
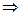
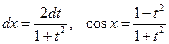 . Имеем:
. Имеем:
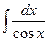 =
= 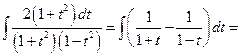
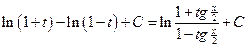 .
.
7.Интегралы вида
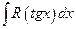 , (4.14)
, (4.14)
где 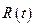 - рациональная функция, удобнее брать с помощью подстановки:
- рациональная функция, удобнее брать с помощью подстановки:
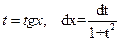 . (4.15)
. (4.15)
Пример. 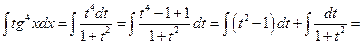
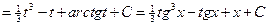 .
.
Интегралы вида
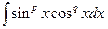 , (4.16)
, (4.16)
где 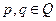 , т.е. рациональные числа, подстановкой
, т.е. рациональные числа, подстановкой
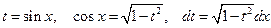 (4.17)
(4.17)
приводятся к интегралам от биномиальных дифференциалов. Действительно,
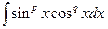 =
= 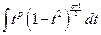 .
.
На основании критерия Чебышева этот интеграл выражается через элементарные функции лишь в трех случаях, когда одно из чисел:
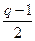 ,
, 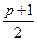 ,
,  (4.18)
(4.18)
является целым числом. В частности, если оба числа 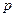 и
и 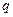 - целые, то это условие выполняется, т.к. если одно (или два) из этих чисел - нечетные, то целым будет
- целые, то это условие выполняется, т.к. если одно (или два) из этих чисел - нечетные, то целым будет 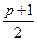 или
или 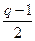 , или все три. Если же p и q - четные числа, то число
, или все три. Если же p и q - четные числа, то число  - целое.
- целое.
Интегралы вида
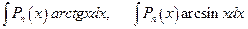 , (4.19)
, (4.19)
где 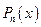 - многочлен степени
- многочлен степени 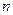 , берутся по частям. Полагают:
, берутся по частям. Полагают:
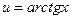 ,
, 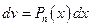 , (4.20)
, (4.20)
или
 ,
, 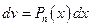 . (4.21)
. (4.21)
Пример. 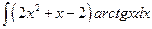 .
.
Положим: 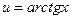 ,
, 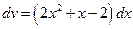 ®
® 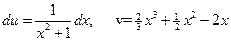 .
.
Следовательно,
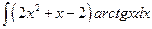 =
= 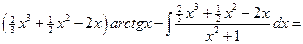
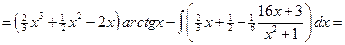
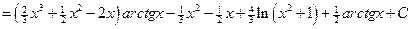 .
.
Аналогичным способом берутся интегралы вида
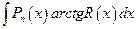 , (4.22)
, (4.22)
где 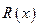 - рациональная функция.
- рациональная функция.
В заключение заметим, что рассмотренные способы интегрирования далеко не исчерпывают все многообразие приемов интегрирования. Из изложенного следует, насколько операция интегрирования сложнее операции дифференцирования. Если продифференцировать можно любую элементарную функцию, то обратная операция - интегрирование даже в принципе иногда не разрешима в элементарных функциях. Такие интегралы называются интегралами не выражающимися в квадратурах. К их числу, например, относятся интегралы:
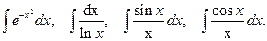 (4.23)
(4.23)
5.2 Определённый интеграл. Формула Ньютона-Лейбница
1. Интегральная сумма Римана. Понятие определённого интеграла
Пусть на отрезке 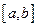 задана непрерывная функция
задана непрерывная функция  .
.
 y
y
M
m
0 a  b x
b x
Обозначим через m и M наименьшее и наибольшее значение функции на отрезке 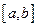 .
.
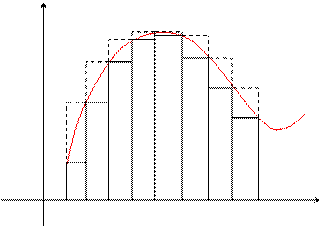
Разобьем отрезок 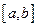 на части (не обязательно одинаковые) n точками:
на части (не обязательно одинаковые) n точками:
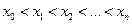 .
.
Введём обознаячения 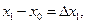
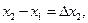 …
… 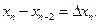 На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции:
На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции:
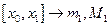 ,
, 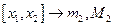 , …
, … 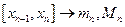 .
.
Составим суммы:
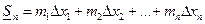 =
= 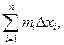
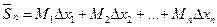 =
=  .
.
Сумма 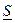 называется нижней интегральной суммой, а сумма
называется нижней интегральной суммой, а сумма 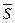 – верхней интегральной суммой, соответствующей данному разбиению отрезка. Так как
– верхней интегральной суммой, соответствующей данному разбиению отрезка. Так как 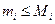 то
то 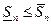 , а
, а  .
.
Внутри каждого отрезка выберем по точке
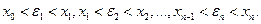
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции  на отрезке
на отрезке 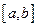
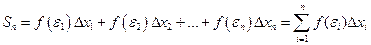 ,
,
соответствующей данному разбиению отрезка на части и данному выбору в этих частях промежуточных точек. Тогда
 .
.
Следовательно,

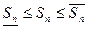 .
.
Обозначим через 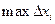 – наибольший отрезок разбиения. Если
– наибольший отрезок разбиения. Если 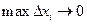 , то число отрезков разбиения отрезка
, то число отрезков разбиения отрезка 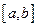 стремится к бесконечности.
стремится к бесконечности.
Определение. Если существует конечный предел 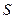 последовательности интегральных сумм
последовательности интегральных сумм 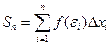 при
при 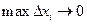 , не зависящий ни от разбиения отрезка
, не зависящий ни от разбиения отрезка 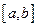 на части ни от выбора в этих частях промежуточных точек, то этот предел называется определённым интегралом от функции
на части ни от выбора в этих частях промежуточных точек, то этот предел называется определённым интегралом от функции  по отрезку
по отрезку 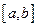 , а функция
, а функция  называется интегрируемой по Риману на отрезке
называется интегрируемой по Риману на отрезке 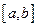 .
.
По определению:
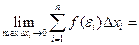

Обозначение: 
Число 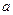 называется нижним пределом интегрирования, а число
называется нижним пределом интегрирования, а число 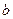 верхним пределом интегрирования;
верхним пределом интегрирования; 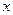 называется переменной интегрирования;
называется переменной интегрирования; 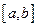 – отрезок интегрирования.
– отрезок интегрирования.
Теорема. Если функция  непрерывна на отрезке
непрерывна на отрезке 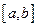 , то она интегрируема на этом отрезке.
, то она интегрируема на этом отрезке.
2. Свойства определенного интеграла
1) 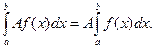
2) 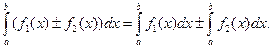
3) 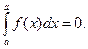
4) Если 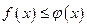 на отрезке
на отрезке 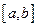
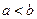 , то
, то 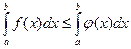 .
.
5) Если  и
и 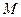 – соответственно наименьшее и наибольшее значения функции
– соответственно наименьшее и наибольшее значения функции  на отрезке
на отрезке 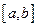 , то:
, то:
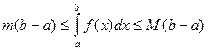 .
.
6) Теорема о среднем. Если функция  непрерывна на отрезке
непрерывна на отрезке 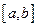 , то на этом отрезке существует точка e такая, что
, то на этом отрезке существует точка e такая, что
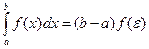 .
.
Доказательство. В соответствии со свойством 5:
 ,
,
так как функция  непрерывна на отрезке
непрерывна на отрезке 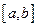 , то она принимает на этом отрезке все свои промежуточные значения
, то она принимает на этом отрезке все свои промежуточные значения  до М. Другими словами, существует такое число
до М. Другими словами, существует такое число 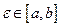 , что если
, что если 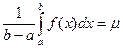 и
и 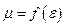 , а
, а 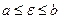 , тогда
, тогда 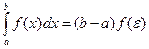 . Теорема доказана.
. Теорема доказана.
7) Для произвольных чисел 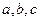 справедливо равенство:
справедливо равенство:
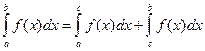 ,
,
при условии существования каждого из входящих в него интегралов.
8) 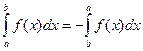
Обобщенная теорема о среднем. Если функции  и
и 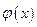 непрерывны на отрезке
непрерывны на отрезке 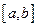 , и функция
, и функция 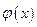 знакопостоянна на нем, то на этом отрезке существует точка e, такая, что
знакопостоянна на нем, то на этом отрезке существует точка e, такая, что
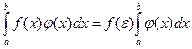 .
.
Дата добавления: 2015-09-29; просмотров: 713;
