Формула прямоугольников

Если известны значения функции 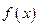в некоторых точках 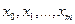, то в качестве функции аппроксимирующей 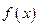можно взять многочлен 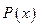степени не выше 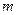, значения которого в выбранных точках равны значениям функции f(x) в этих точках.

.

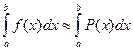Разобьем отрезок интегрирования на 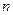равных частей и положим 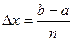. При этом:

, …. , .

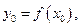
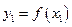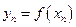Составим суммы 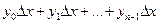; 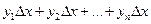- соответственно нижнюю и верхнюю интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной. Тогда

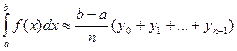или -

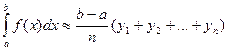любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.