Формула парабол
(формула Симпсона или квадратурная формула).
Разделим отрезок интегрирования 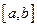 на четное число отрезков
на четное число отрезков 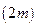 . Площадь криволинейной трапеции, ограниченной графиком функции
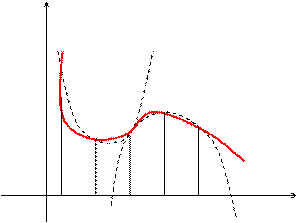
. Площадь криволинейной трапеции, ограниченной графиком функции 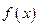 заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями
заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями 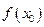 ,
, 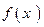 ,
, 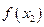 . Для каждой пары отрезков построим такую параболу.
. Для каждой пары отрезков построим такую параболу.
 |
0 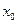
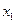
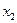
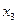
 х
х
Уравнения этих парабол имеют вид 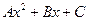 , где коэффициенты
, где коэффициенты 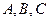 могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
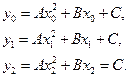 (6.1)
(6.1)
Обозначим 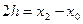 .
.
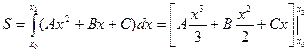 .
.
Если принять 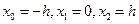 , то
, то 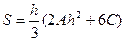 (6.2)
(6.2)
Тогда уравнения значений функции (6.1) имеют вид:
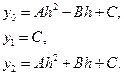
C учетом этого: 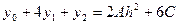 .
.
Отсюда уравнение (6.2) примет вид: 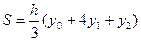 .
.
Тогда
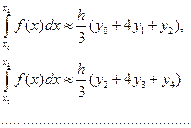
Складывая эти выражения, получаем формулу Симпсона:
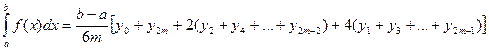 .
.
Чем больше взять число 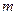 , тем более точное значение интеграла будет получено.
, тем более точное значение интеграла будет получено.
Пример. Вычислить приближенное значение определенного интеграла
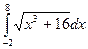 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
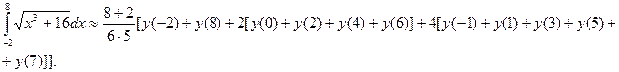
| m | |||||||||||
| x | -2 | -1 | |||||||||
| f(x) | 2.828 | 3.873 | 4.123 | 4.899 | 6.557 | 8.944 | 11.874 | 15.232 | 18.947 | 22.978 |
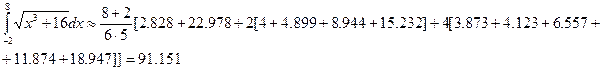
Точное значение этого интеграла – 91.173.
Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.
Для сравнения применим к этой же задаче формулу трапеций.
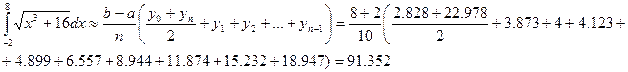 Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
Кроме вышеперечисленных способов, можно вычислить значение определенного интеграла с помощью разложения подынтегральной функции в степенной ряд.
Принцип этого метода состоит в том, чтобы заменить подынтегральную функцию по формуле Тейлора и почленно проинтегрировать полученную сумму.
Пример. С точностью до 0,001 вычислить интеграл
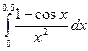 .
.
Так как интегрирование производится в окрестности точки 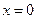 , то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.
, то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.
Разложение функции 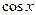 имеет вид:
имеет вид:
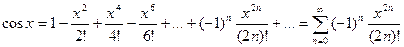 .
.
Зная разложение функции 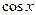 легко найти функцию
легко найти функцию 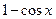 :
:
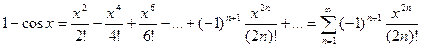 .
.
Теперь представим в виде ряда подынтегральное выражение:
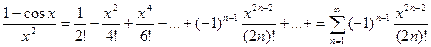 .
.
Теперь представим наш интеграл в виде:
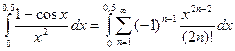 .
.
Применим теорему о почленном интегрировании ряда. (Т.е. интеграл от суммы будет представлен в виде суммы интегралов членов ряда).
Вообще говоря, со строго теоретической точки зрения для применения этой теоремы надо доказать, что ряд сходится равномерно на отрезке интегрирования 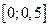 .
.
Таким образом
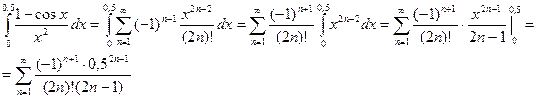
Получаем:
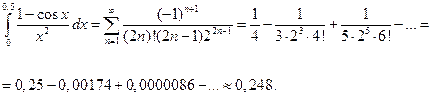
Как видно, абсолютная величина членов ряда очень быстро уменьшается, и требуемая точность достигается уже при третьем члене разложения.
Более точное значение этого интеграла: 0,2482725418…
5.3 Геометрические приложения определённого интеграла
Дата добавления: 2015-09-29; просмотров: 1020;
