Пример. , с другой стороны, если применить тригонометрическую подстановку,
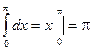 , с другой стороны, если применить тригонометрическую подстановку,
, с другой стороны, если применить тригонометрическую подстановку,
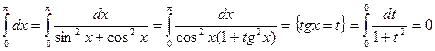 ,
,
т. е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная 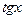 имеет на отрезке интегрирования разрыв (в точке
имеет на отрезке интегрирования разрыв (в точке 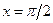 ). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
5. Интегрирование по частям определённого интеграла
Если функции 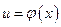 и
и 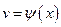 непрерывны на отрезке
непрерывны на отрезке 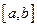 вместе со своими производными, то справедлива формула интегрирования по частям:
вместе со своими производными, то справедлива формула интегрирования по частям:
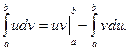
Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше.
Дата добавления: 2015-09-29; просмотров: 1002;
