Для уяснения возможности применения уравнений Лагранжа при составлении динамических уравнений СИ рассмотрим пример.

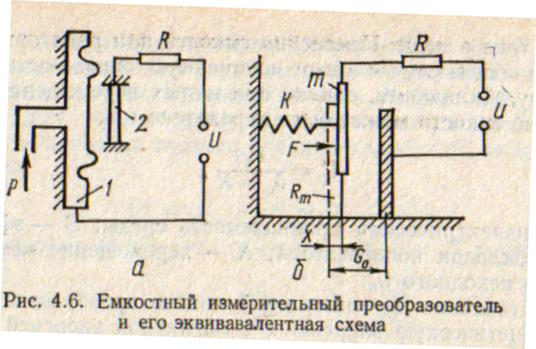
Емкостный измерительный преобразователь (рис. 4.6, а) давле­ния р состоит из конденсатора, образованного неподвижной обклад­кой 2 и мембраной R, подключенного через сопротивление к ис­точнику напряжения и. Схематическое изображение основных элементов емкостных преобразователей показано на рис. 4.6, б. Необходимо учесть два эффекта: механический и электрический. Механическое перемещение мембраны эквивалентно перемещению массы m под действием силы F, ограниченному упругой силой пру­жины (мембраны) k. Демпфирующее действие объема воздуха между мембраной и неподвижной обкладкой учитывается коэффициентом демпфирования 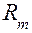. Перемещение мембраны приводит к изменению емкости и тока в цепи. Изменения емкости или реактивного сопро­тивления в обіцем случае имеют нелинейную зависимость от рассто­яния между обкладками, однако при малых перемещениях мембра­ны значение емкости 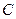может быть определено как

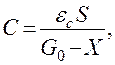
где 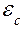— диэлектрическая проницаемость среды; S — эффективная площадь обкладок конденсатора; X — перемещение мембраны от­носительно исходной координаты .

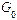Для составления математической модели преобразователя отож­дествим кинетическую энергию Т с магнитной энергией 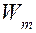, а по­тенциальную П — с электрической .

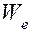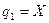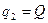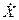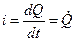Обобщенные координаты при этом будут: перемещение и заряд , а обобщенные скорос­ти — и ток . Обобщенные силы: сила 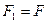, создаваемая давлением 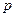, подаваемым в мембранную коробку, и 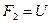– напряжение, поданное на схему.

В общем случае силовые функции, входящие в уравнения Лагранжа (4.61), необходимо определять путем инте­грирования по уравнениям (4.52), (4.55) и (4.39). Для линейного преобразователя силовые функции могут быть определены как квад­ратичные функции координат и скоростей.

Кинетическая энергия равна механической (магнитная равна нулю):

_.

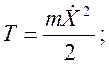Потенциальная энергия состоит из запасенных энергий пружи­ны и конденсатора:

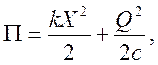
или с учетом выражения для емкости:

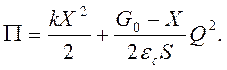
Функция рассеяния:

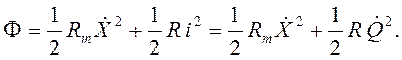
Применив уравнения Лагранжа (4.61) для обобщенных координат X и ,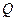

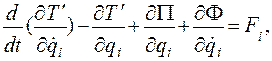(4.61)

получим два уравнения:

_,

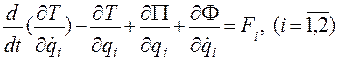которые при подстановке соответствующих обобщенных координат и обобщенных сил примут вид:

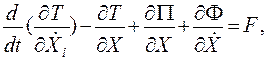(4.61,а)

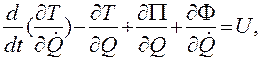(4.61,б)

Рассмотрим члены, входящие в уравнения (4.61,а), (4.61,б).

; ; ;

; ;

; ; ; .

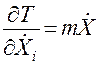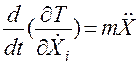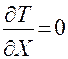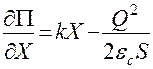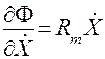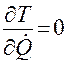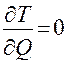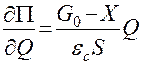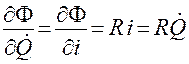Подставляя полученные выражения в (4.61,а), (4.61,б) имеем:

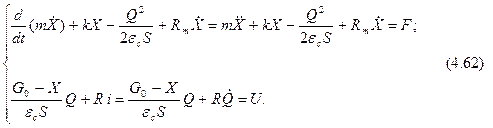
Заряд Q и перемещение X удобно представить как

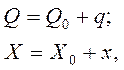
где Х₀ — установившееся значение перемещения при F = 0, но при подключенном источнике напряжения; 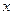— перемещение мембраны относительно установившегося значения X (рис. 4.6, б).

При малых перемещениях 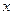и изменениях q в сравнении с Х₀ и Q₀, когда величинами второго порядка малости q², qх и т. д. можно пренебречь,

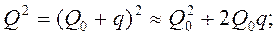
тогда уравнения (4.62) с учетом значений Q и X примут вид

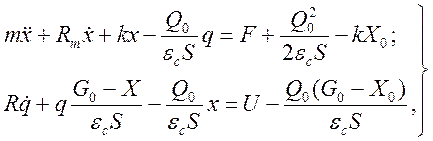
С учетом условий равновесия, определяемого для Q₀ и Х₀, (при )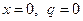

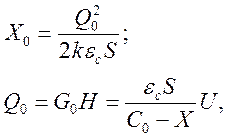
окончательно можно записать динамические уравнения преобразо­вателя:

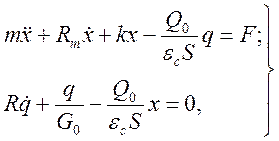(4.63)

Дифференциальные уравнения (4.63) полностью описывают дина­мические процессы в емкостном преобразователе. Аналогичным об­разом можно получить уравнения, например, электромагнитных, индуктивных, индукционных и других преобразователей или же СИ в целом.

Порядок получения уравнений для любой измерительной цепи при этом следующий:

- выбирают систему обобщенных переменных и определяют внеш­ние силы за счет источников;

- определяют кинетическую и потенциальную энергии цепи в це­лом ;

-определяют силы, связанные с рассеянием, и записывают функ­цию Рэлея;

- подставляют выражения энергий и функций Рэлея в уравнения Лагранжа и, выполняя дифференцирование по каждой обобщенной координате и скорости, получают п динамических уравнений.

В случае сложной измерительной цепи возникает целый ряд трудностей: выбор независимых обобщенных координат; отождест­вление энергий; определение количества обобщенных координат; определение и преобразование силовых функций и др.