ПРИНЦИП ГАМИЛЬТОНА И УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
В механических системах для нахождения связи между силами и перемещениями, которые во многих случаях являются входными и выходными величинами СИ, широко используются уравнения Лагранжа второго рода [45]. Использование уравнений Лагранжа является примером применения одного из интегральных принципов для описания динамики систем. Наиболее фундаментальным интегральным принципом считают принцип Гамильтона [42], суть которого состоит в том, что вариация интеграла по времени от функции Лагранжа L между двумя фиксированными точками 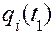 и
и 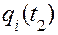 должна равняться нулю:
должна равняться нулю:
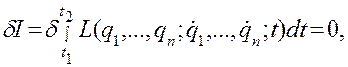
где 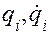 — обобщенные координаты и обобщенные скорости;
— обобщенные координаты и обобщенные скорости; 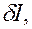 — вариация интеграла функции Лагранжа.
— вариация интеграла функции Лагранжа.
Принцип Гамильтона в дифференциальной форме имеет вид [42]
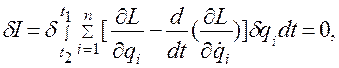 (4.45)
(4.45)
который при всех независимых 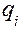 дает уравнения Лагранжа второго рода для консервативной системы:
дает уравнения Лагранжа второго рода для консервативной системы:
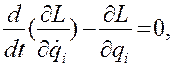 (4.46)
(4.46)
Уравнения Лагранжа (4.46) с силовой функцией Лагранжа L определяют динамическую траекторию системы, включая условия связи, например электромеханической. Использование принципа Д'Аламбера и законов Кирхгофа в данном случае излишне. Кроме того, функция Лагранжа и другие силовые функции имеют основное значение для характеристик физических систем: электрических, механических, электромеханических, химических, термодинамических и др.
Энергетические функции обычно являются силовыми, поскольку зависят, как правило, от состояния системы в данный момент, а не от предыстории. Эти функции, несмотря на различную физическую природу, имеют фундаментальную общность и приводятся к единой математической трактовке. Например, уравнение изменения энергии для механической системы
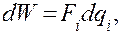 (4.47)
(4.47)
где 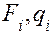 — сила и перемещение (координата).
— сила и перемещение (координата).
Они описывают энергетические соотношения и в других системах, если считать, что 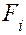 и
и 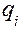 — обобщенные переменные. Действительно, такими переменными в системах могут быть: в тепловой — температура и энтропия; в электрической — напряжение и заряд; в химической — химический потенциал и число молей и т. д. Таким образом, налицо замечательное свойство аналогии многих природных явлений, которое выражается в том, что количественные закономерности могут совпадать для явлений, совершенно разных физически. Разные по своей природе процессы переноса количества движения, массы, теплоты и электричества подчиняются одинаковым количественным закономерностям и соответствующие физические величины и параметры этих процессов являются аналогами.
— обобщенные переменные. Действительно, такими переменными в системах могут быть: в тепловой — температура и энтропия; в электрической — напряжение и заряд; в химической — химический потенциал и число молей и т. д. Таким образом, налицо замечательное свойство аналогии многих природных явлений, которое выражается в том, что количественные закономерности могут совпадать для явлений, совершенно разных физически. Разные по своей природе процессы переноса количества движения, массы, теплоты и электричества подчиняются одинаковым количественным закономерностям и соответствующие физические величины и параметры этих процессов являются аналогами.
Следовательно, получив энергетическую (силовую) функцию для системы любой физической природы и отождествив, например, обобщенные переменные, силы и координаты, для описания динамики этих систем можно использовать интегральный принцип (принцип Гамильтона, уравнения Лагранжа и др.).
Силовая функция Лагранжа в классической механике [45] — это функция системы координат 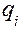 системы скоростей
системы скоростей 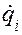 и времени t:
и времени t:
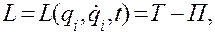 (4.48)
(4.48)
где Т — кинетическая энергия; П — потенциальная энергия. Лагранжиан (4.48) не описывает общий случай, так как не позволяет прямо распространить его на нелинейные системы. Это связано с тем, что независимые переменные 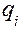 и
и 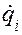 не являются функциями еще двух переменных: обобщенной силы
не являются функциями еще двух переменных: обобщенной силы 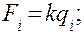 обобщенного импульса
обобщенного импульса 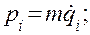 . Для линейных систем коэффициенты k и т постоянны и замена
. Для линейных систем коэффициенты k и т постоянны и замена 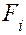 и
и 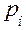 на
на 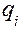 и
и 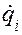 не влияет на первоначальный выбор системы независимых переменных. Для нелинейных систем
не влияет на первоначальный выбор системы независимых переменных. Для нелинейных систем 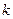 и
и 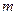 обычно являются функциями переменных, поэтому такая замена должна производиться с учетом выбора независимых координат.
обычно являются функциями переменных, поэтому такая замена должна производиться с учетом выбора независимых координат.
С целью распространения лагранжиана на нелинейные системы разложим его на две функции. Полный дифференциал лагранжиана
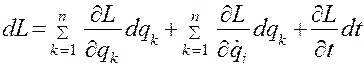 (4.49)
(4.49)
Поскольку L — силовая функция и ее конечное значение не зависит от пути интегрирования, представляется возможным выполнить интегрирование (4.49) при постоянном времени t для условий: при интегрировании по 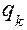 все
все 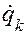 постоянны или же равны нулю; при интегрировании по
постоянны или же равны нулю; при интегрировании по 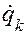 все
все 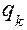 постоянны. Тогда из уравнения (4.49)
постоянны. Тогда из уравнения (4.49)
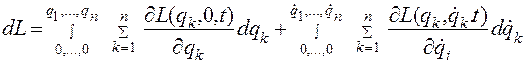 (4.50)
(4.50)
Первое слагаемое этого уравнения является функцией только 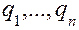 и
и 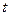 и для линейных систем равно потенциальной энергии, взятой со знаком минус. Однако при интегрировании не накладывалось условие линейности, поэтому полученное выражение справедливо и для нелинейных систем, то есть в общем случае обобщенная сила (потенциальная)
и для линейных систем равно потенциальной энергии, взятой со знаком минус. Однако при интегрировании не накладывалось условие линейности, поэтому полученное выражение справедливо и для нелинейных систем, то есть в общем случае обобщенная сила (потенциальная)
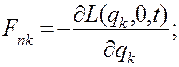 (4.51)
(4.51)
потенциальная энергия
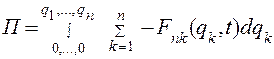 (4.52)
(4.52)
Потенциальная энергия для механических линейных стационарных систем [45] является однородной квадратичной функцией координат:
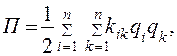 (4.53)
(4.53)
где 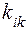 — постоянные коэффициенты, имеющие смысл и размерность упругости.
— постоянные коэффициенты, имеющие смысл и размерность упругости.
Обобщенные силы потенциального поля
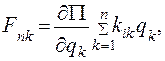 (4.54)
(4.54)
Второе слагаемое уравнения (4.50)—функция конечных значений координат 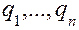 и скоростей
и скоростей 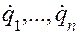 и для линейного случая соответствует кинетической энергии или запасенной магнитной энергии (при
и для линейного случая соответствует кинетической энергии или запасенной магнитной энергии (при 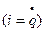 . В нелинейном случае второе слагаемое представляет собой кинетическую коэнергию
. В нелинейном случае второе слагаемое представляет собой кинетическую коэнергию 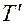 :
:
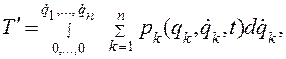 (4.55)
(4.55)
где 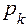 — обобщенный импульс кинетических потенциалов,
— обобщенный импульс кинетических потенциалов,
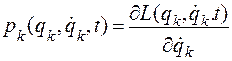 . (4.56)
. (4.56)
Следует отметить, что на практике кинетическую энергию чаще определяют путем интегрирования по обобщенным скоростям 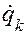 , чем по обобщенным импульсам. При этом кинетическую энергию получить проще, чем кинетическую коэнергию.
, чем по обобщенным импульсам. При этом кинетическую энергию получить проще, чем кинетическую коэнергию.
Для механических линейных стационарных систем кинетическая энергия (Т = Т') может быть представлена [45] в виде однородной квадратичной функции скоростей:
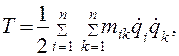 (4.57)
(4.57)
где 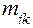 — постоянные коэффициенты, характеризующие инерционность и имеющие смысл и размерность массы.
— постоянные коэффициенты, характеризующие инерционность и имеющие смысл и размерность массы.
Обобщенная i-я сила, вызванная изменением кинетической энергии системы,
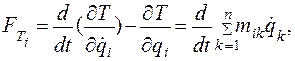 (4.58)
(4.58)
Уравнения Лагранжа второго рода (4.46), Лагранжиан (4.48) и полученные соотношения для определения энергий реальных систем необходимо дополнить диссипативной функцией Рэлея, отражающей необратимые потери энергии, например нагрев активных сопротивлений, нагрев тел за счет трения и т. д. Для линейных систем
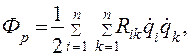 (4.59)
(4.59)
где 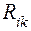 — коэффициенты, имеющие смысл и размерность сопротивления.
— коэффициенты, имеющие смысл и размерность сопротивления.
Силы рассеяния
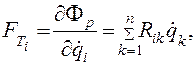 (4.60)
(4.60)
Тогда окончательно уравнения Лагранжа (4.46), устанавливающие связь между изменениями энергий внутри системы и внешними обобщенными силами, имеют вид
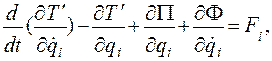 (4.61)
(4.61)
где 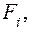 — i-я внешняя сила, действующая на систему.
— i-я внешняя сила, действующая на систему.
Эти уравнения полностью определяют движение системы, если известны значения энергий Т' или Т, П и Ф. Кроме того, эти уравнения можно распространить на электрические и электромеханические системы или измерительные цепи, отождествив, например, кинетическую энергию Т с магнитной 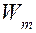 , а потенциальную П — с электрической
, а потенциальную П — с электрической 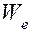
ПРИМЕР ДЛЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ
Дата добавления: 2015-11-18; просмотров: 1643;
