Интегрирование дробно-рациональных функций
Разложение правильной рациональной дроби на простейшие.
Пусть 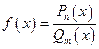 - дробно-рациональная функция, где
- дробно-рациональная функция, где 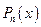 и
и 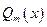 - многочлены соответственно степеней
- многочлены соответственно степеней 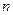 и
и 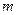 .
.
Если 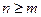 , то, разделив многочлен
, то, разделив многочлен 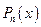 на
на 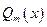 , представим дробно-рациональную функцию
, представим дробно-рациональную функцию 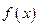 в виде:
в виде:
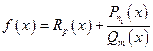 , (3.1)
, (3.1)
где 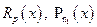 - многочлены степеней
- многочлены степеней 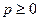 и
и 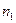 , причем
, причем 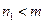 . Дробь
. Дробь 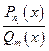 называется правильной рациональной дробью.
называется правильной рациональной дробью.
Так как произвольный многочлен интегрируется по формуле (1.15), то интегрирование дробно-рациональных функций сводится к интегрированию правильных рациональных дробей.
Известно, что всякий многочлен с действительными коэффициентами разлагается в произведение неприводимых множителей только первой и второй степени, причем в случае кратных корней эти множители могут в разложении присутствовать в степени выше первой. В алгебре доказывается важная теорема: всякая правильная рациональная дробь разлагается единственным образом в сумму конечного числа простейших дробей вида:
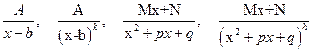 ,
, 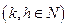 , (3.2)
, (3.2)
причем, если, например, 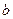 -
- 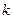 -кратный корень знаменателя
-кратный корень знаменателя 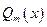 , то в разложении соответствующая этому корню сумма записывается в виде:
, то в разложении соответствующая этому корню сумма записывается в виде:
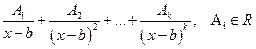 . (3.3)
. (3.3)
Аналогично, если в разложении знаменателя неприводимый квадратный трехчлен 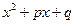
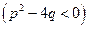 входит в степени
входит в степени 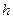 , то соответствующий этому трехчлену сумма имеет вид:
, то соответствующий этому трехчлену сумма имеет вид:
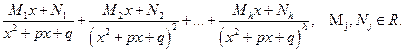 (3.4)
(3.4)
Для определения коэффициентов разложения приводят сумму к общему знаменателю 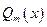 и тождественно приравнивают полученный числитель данному числителю
и тождественно приравнивают полученный числитель данному числителю 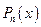
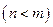 . Получается система
. Получается система 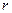 линейных уравнений с
линейных уравнений с 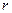 неизвестными коэффициентами и отличным от нуля определителем. По правилу Крамера находят все коэффициенты разложения.
неизвестными коэффициентами и отличным от нуля определителем. По правилу Крамера находят все коэффициенты разложения.
Пример. Разложить на простейшие дроби правильную рациональную дробь
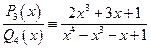 . (3.5)
. (3.5)
1) Разлагаем на неприводимые множители знаменатель 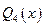 :
:
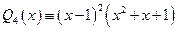 . (3.6)
. (3.6)
2) Записываем разложение данной рациональной дроби на простейшие с неопределенными коэффициентами:
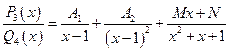 . (3.7)
. (3.7)
3) Приводим правую часть к общему знаменателю:
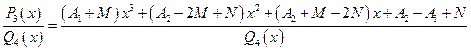 . (3.8)
. (3.8)
4) Приравнивая тождественно числители, получим:
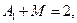
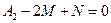 ,
, 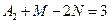 ,
, 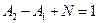 . (3.9)
. (3.9)
5) Решаем систему четырех линейных уравнений с четырьмя неизвестными:
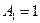 ,
, 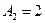 ,
, 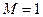 ,
, 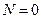 . (3.10)
. (3.10)
6) Записываем разложение (3.7) с найденными значениями коэффициентов:
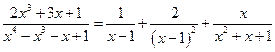 . (3.11)
. (3.11)
Следовательно, интегрирование дробно-рациональных функций сводится к интегрированию полиномов и простейших рациональных дробей (3.2). Имеем:
1) 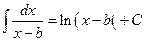 , (3.12)
, (3.12)
2) 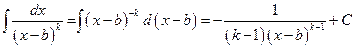 ,
, 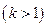 , (3.13)
, (3.13)
3) 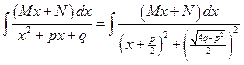 .
.
Положим 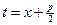 ,
, 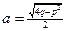 . Тогда
. Тогда
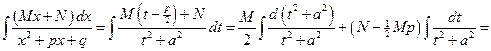
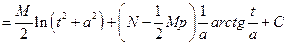 .
.
Следовательно,
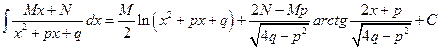 . (3.14)
. (3.14)
4) 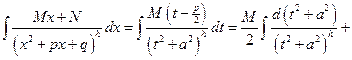
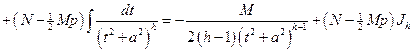
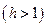 ,
,
где интеграл
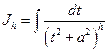 (3.15)
(3.15)
вычисляется по рекуррентной формуле:
 . (3.16)
. (3.16)
Действительно,
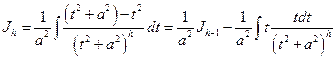 .
.
Обозначим: 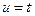 ,
, 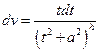 ®
® 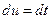 ,
,
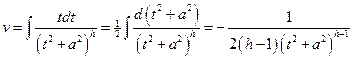 .
.
Следовательно,
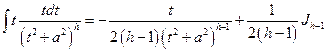 ,
,
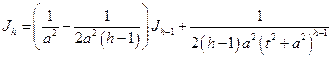 ,
,
т.е. справедлива формула (3.16).
Рассмотрим несколько примеров.
№1. 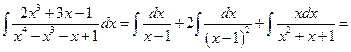
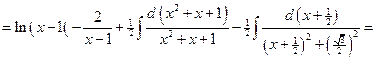
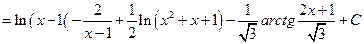 .
.
Здесь мы воспользовались формулой (3.11) разложения подынтегральной функции на простейшие дроби.
№2. 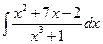 .
.
1) Разлагаем подынтегральную функцию на простейшие дроби:
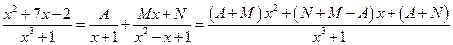 .
.
Следовательно,
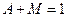 ,
, 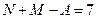 ,
, 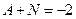 .
.
Решая эту систему, находим:
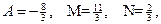
т.е.
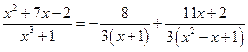 .
.
2) Осуществляем интегрирование:
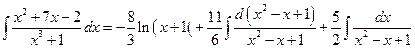 =
=
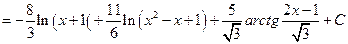 .
.
№3. 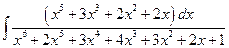 .
.
1) Разлагаем знаменатель 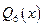 подынтегральной функции на неприводимые множители:
подынтегральной функции на неприводимые множители:
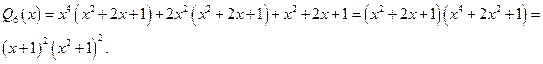
2) Разлагаем подынтегральную функцию 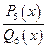 на простейшие дроби:
на простейшие дроби:
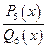 =
= 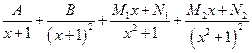 =
=
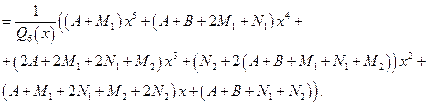
Приравнивая тождественно числитель многочлену
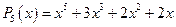
и решая полученную систему линейных уравнений, находим:
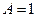 ,
, 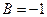 ,
, 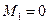 ,
, 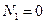 ,
, 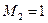 ,
, 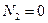 .
.
Следовательно,
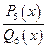 =
= 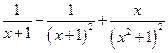 ;
;
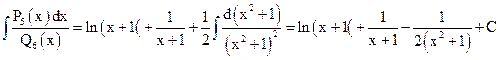 .
.
Дата добавления: 2015-09-29; просмотров: 1256;
