Тема 2.5 Определенный интеграл.
2.51 Понятие определенного интеграла,
его геометрический смысл.
Задача о площади криволинейной трапеции.
Пусть на отрезке [a;b] задана неотрицательная функция y=f(x). Требуется найти площадь S криволинейной трапеции, ограниченной кривой y=f(x), прямыми x=a, x=b и осью у=0
(рис. 10).








 у y= f(x) y y=f(x) ломаная
у y= f(x) y y=f(x) ломаная
 | |||
 | |||


S Sл

 0 a b x 0 a b x
0 a b x 0 a b x
Рис.10 рис.11
Наметим общий подход к решению этой задачи. Введем в рассмотрение некоторую ломаную, которая расположена достаточно близко к кривой y= f(x) на [a;b] (рис.11) . фигура под ломаной состоит из трапеций ( прямоугольников) , и ее площадь Sл ( равная сумме площадей этих трапеций) может быть вычислена с использованием известных формул планиметрии. Поскольку ломаная выбрана достаточно близко к кривой y=f(x), то справедливо приближенное равенство S≈ Sл. Это равенство оказывается тем более точным, чем ближе расположена ломаная к исходной кривой. Поэтому естественно за искомую площадь S взять предел площади Sл под ломаной в предположении неограниченного приближения ломаной к заданной кривой.
Приведенные рассуждения носят качественный характер. Для того чтобы их можно было использовать на практике, необходимо уточнить в них то, что описывалось нестрого: процедура выбора ломаной и последующий предельный переход. На этом пути мы получим понятие определенного интеграла.
Понятие интегральной суммы.
Пусть на [a;b] задана функция у=f(x). Разобьем отрезок [a;b] на n элементарных отрезков точками x0, x1,…, xn: a=x0<x1<x2<…<xn=b. На каждом отрезке [xi-1,xi] разбиения выберем некоторую точку ξi и положим Δ xi=xi-xi-1, где i=1,2,3,…,n. Сумму вида
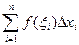
будем называть интегральной суммой для функции y=f(x) на [a;b]. Очевидно, что интегральная сумма зависит как от способа разбиения отрезка [a;b] точками x0, x2, …, xn, так и от выбора точек ξ1, ξ2, … ξn на каждом из отрезков разбиения [x i-1, xi], где
i=1, 2, … n.
Геометрический смысл интегральной суммы.
Пусть функция y= f(x) неотрицательна на [a;b] . отдельное слагаемое f(ξi).Δxi интегральной суммы в этом случае равно Si прямоугольника со сторонами f(ξi) и Δxi, где i=1, 2, … n ( см. рис. 12, где х0-х1= Δx1, х2-х1= Δx2, и т.д.)
|


 y y=f(x)
y y=f(x)



 f(ξ3)
f(ξ3)
f(ξ2) 



f(ξ1) 



0 a=x0 ξ1 x1 ξ2 x2 ξ3  x3 x
x3 x
Рис.12
ванной на каждом из отрезков [xi-1,xi] прямой y= f(ξ i) параллельной оси абсцисс ( рис.12)
Понятие определенного интеграла.
Для избранного разбиения отрезка [a;b] на части обозначим через
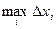 максимальную из длин отрезков [xi-1,xi], где i=1, 2, … n.
максимальную из длин отрезков [xi-1,xi], где i=1, 2, … n.
Определение.Пусть предел интегральной суммы при стремлении 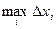 к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек ξ1, ξ2, … .Тогда этот предел называется определенным интегралом от функции y=f(x) на [a,b], обозначается
к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек ξ1, ξ2, … .Тогда этот предел называется определенным интегралом от функции y=f(x) на [a,b], обозначается 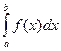 , а сама функция y=f(x) называется интегрируемой на отрезке [a,b], т.е.
, а сама функция y=f(x) называется интегрируемой на отрезке [a,b], т.е.
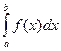 =
= 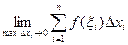 .
.
При этом число а называется нижним пределом, число b- его верхним пределом; функция f(x) - подынтегральной функцией, выражениеf(x)dx- подынтегральным выражением, а задача о нахождении 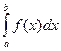 - интегрированием функции f(x) на отрезке [a,b].
- интегрированием функции f(x) на отрезке [a,b].
Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия: в то время как 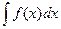 - представляет семейство функций,
- представляет семейство функций, 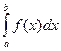 - есть определенное число.
- есть определенное число.
Геометрический смысл определенного интеграла.
Понятие определенного интеграла введено таким образом , что в случае, когда функция y=f(x) неотрицательна на отрезке [a,b], где a<b, 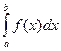 численно равен площади S под кривой y=f(x) на [a,b] (см. рис. 10). Действительно, при стремлении
численно равен площади S под кривой y=f(x) на [a,b] (см. рис. 10). Действительно, при стремлении 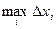 к нулю ломаная (см. рис.12) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
к нулю ломаная (см. рис.12) неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
2.52 Свойства определенного интеграла.
Формула Ньютона-Лейбница.
Свойства определенного интеграла:
1.Постоянный множитель можно выносить за знак интеграла, т.е
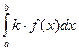 =k
=k 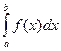 ,
,
где k- некоторое число.
2.Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
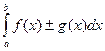 =
= 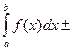
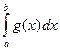 .
.
3.Если отрезок интегрирования разбит на части , то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b, с:
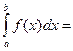
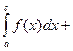
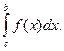
Формула Ньютона –Лейбница:
Основная формула интегрального исчисления, традиционно связана с именами И. Ньютона и Г. Лейбница.
Теорема. Пусть функция y=f(x) непрерывна на отрезке [a,b] и F(x) –любая первообразная для f(x) на [a,b]. Тогда определенный интеграл от функции f(x) на [a,b] равен приращению первообразной F(x) на этом отрезке, т.е.
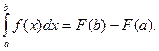
Следует подчеркнуть, что при применении формулы Ньютона- Лейбница можно использовать любую первообразную F(x) для подынтегральной функции f(x).например, имеющую наиболее простой вид при С=0.
Например. Вычислить: а) 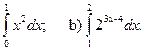
Решение :
а) произвольная первообразная для функции f(x)=х2 имеет вид 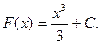 для нахождения интеграла по формуле Ньютона- Лейбница возьмем такую первообразную, у которой С=0. Тогда
для нахождения интеграла по формуле Ньютона- Лейбница возьмем такую первообразную, у которой С=0. Тогда

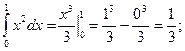
Ответ : 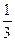 .
.
b) первообразную подынтегральной функции найдем, используя формулу (4). Применяя формулу Ньютона- Лейбница получаем
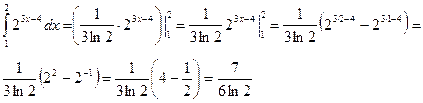
Ответ: 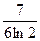 .
.
2.53 Вычисление площадей плоских фигур.
1 способ2 способ






 у y y=f1(x)
у y y=f1(x)



 у=f(x)
у=f(x)
 |
S


 y=f(x)
y=f(x)

 х
х
0 х=а х=b 0 x=a x=b x
f2(x)<f1(x)

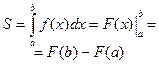
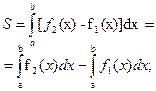
3 способ
 y
y
 y=f(x)
y=f(x)







 y=k
y=k
S
 0 x=a x=b x
0 x=a x=b x
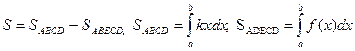 .
.
Рис.13Площади плоских фигур
Например . Вычислить площадь фигуры ограниченной линиями:
а) 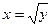 , х=0, у=4; б) у= х2-2, у=х.
, х=0, у=4; б) у= х2-2, у=х.
а)
|
 у
у






 В у=4
В у=4
А
х =0 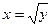
 С
С
О х
1. найдем пределы интегрирования: 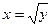
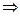 у1=х2 и у2=4
у1=х2 и у2=4
у1=у2;
х2=4 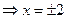 (отрицательный корень не принимаем);
(отрицательный корень не принимаем);
2. SОАВС= 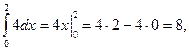
SОВС= 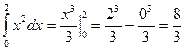 .
.
Окончательно S= 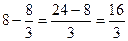 (кв.ед.)
(кв.ед.)
Ответ : S= 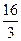 кв.ед.
кв.ед.
б) у
 |
| |||

у1=х2-2 у2=х 
 |

 -1 0
-1 0 

 2 х
2 х
-2
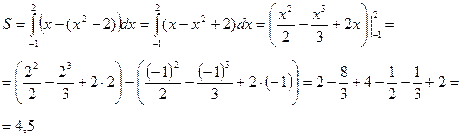
Ответ: S= 4,5 кв.ед.
Упражнения:
1.Вычислить определенный интеграл:
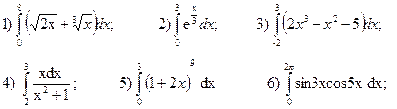
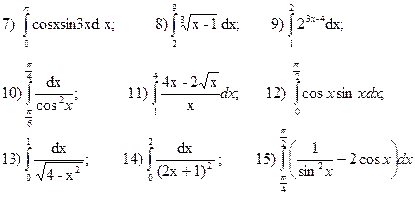
2.Вычислить площадь фигуры ограниченной линиями
1) у= 4-х2; у= 0; 2) у= -х2; х+у+2=0; 3) у= х2; ух=8; у=6;
2) у= 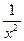
 ; у= х ; х=2; 5) у= ех; у=е-х; у=4.
; у= х ; х=2; 5) у= ех; у=е-х; у=4.
Дата добавления: 2015-11-04; просмотров: 986;
