Тема 2.6 Производная высшего порядка.

До сих пор мы рассматривали производную f^/(x) от функции f(x), называемую производной первого порядка. Но производная f^/(x) сама является функцией, которая также может иметь производную.

Производной n-го порядка называется производная от производной (n-1)-го порядка.

Обозначение производных: f^//(x) –второго порядка (или вторая производная),f^///(x)-третьего порядка( или третья производная).

Для обозначения производных более высшего порядка используются арабские или римские цифры, например,

f⁽⁴⁾(x),…, f ⁿ (x) или f^IV(x) и т.д.

Механический смысл второй производной. Выше было установлено, что если s= s(t) –это закон по которому движется точка, то s^/(t) представляет скорость изменения пути в момент t₀. следовательно, вторая производная пути по времени s^//(t₀)=[s^/(t₀)]^/=ν ^/(t₀) есть скорость изменения скорости или ускорение точки в момент t₀.

Пример. Найти производные до n-го порядка включительно от функции у= ln x.

Решение: 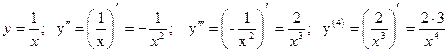и

т . д. очевидно , что производная n-го порядка .

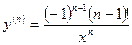Упражнения :

Найти производные: а) второго порядка: 1) у= sin²x, 2) y= tg x, 3) y= ;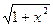

б) третьего порядка: 1) у= x ln x, 2) y= x sin x;

г) n-го порядка: 1) у= ln x, 2) y= sin x, 3) y= xⁿ, 4) у=а^х.