Тема 3.4 Знакочередующиеся ряды.
Под знакочередующимся рядом понимают ряд, в котором члены попеременно то положительны, то отрицательны:
u1-u2+u3-u4+…+(-1)n-1un+… , un>0.
Теорема (признак Лейбница).Если члены знакочередующегося ряда убывают по абсолютной величине u1>u2…>un>… и предел его общего члена при n 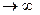 равен нулю, т.е
равен нулю, т.е 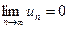 , то ряд сходиться, а его сумма не превосходит первого члена S≤u1.
, то ряд сходиться, а его сумма не превосходит первого члена S≤u1.
Пример. Исследовать сходимость ряда
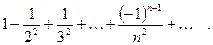
Решение :
Так как члены знакочередующегося ряда убывают по абсолютной величине 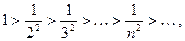 и предел общего члена
и предел общего члена 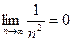 , то по признаку Лейбница ряд сходиться.
, то по признаку Лейбница ряд сходиться.
Определение 1. Ряд называется условно сходящимся, если сходиться как сам ряд , так и ряд, составленный из абсолютных величин его членов.
Определение 2.ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Упражнения:
I.Установить сходимость или расходимость ряда с помощью признаков сравнения:
1) 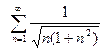 ; 2)
; 2) 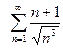 ; 3)
; 3) 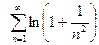 ;
;
4) 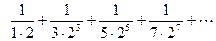 ; 5)
; 5) 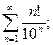
6) 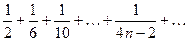
II.Исследовать сходимость ряда с помощью признака Даламбера:
1)  2)
2)  ; 3)
; 3)  ; 4)
; 4) 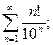
5) 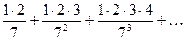
Дата добавления: 2015-11-04; просмотров: 594;
