Знакочередующиеся ряды

Ряд вида 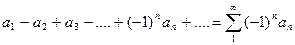, где (5) называется знакочередующимся рядом.

Признак Лейбница. Если члены ряда (5) по модулю монотонно убывают с ростом 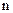, то есть 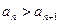, начиная с некоторого n и 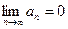, то ряд (5) сходится . Если нарушено хотя бы одно из указанных условий, то ряд расходится.

Пример. Даны числовые ряды:

А)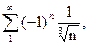

В)

Выяснить характер сходимости этих рядов. Ответ. А сходится, В расходится.

Решение. Для ряда А модулем общего члена ряда является . Ясно, что он монотонно уменьшается , начиная с n=1, 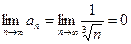. Условия признака Лейбница выполнены, следовательно ряд А сходится.

Для ряда В модулем общего члена ряда является . Очевидно, что второе условие признака Лейбница не выполнено, так как 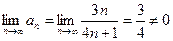, следовательно ряд В расходится.

Определение. Знакочередующийся ряд сходится абсолютно, если сходится ряд составленный из абсолютных значений его членов, то есть если сходится ряд .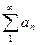

Утверждение. Если знакочередующийся ряд сходится абсолютно, то он просто сходится, то есть справедлива схема:

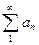-сходится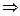 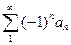- сходится

Определение. Если ряд 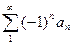сходится, а ряд 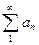расходится ( расходится абсолютно), то говорят, что ряд 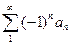сходится условно.

Пример. Укажите правильное утверждение относительно сходимости знакочередующихся рядов:

А) 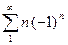и В) 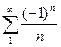. Ответ. А расходится, В сходится условно.

Обоснование. 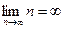, то есть нарушено второе условие признака Лейбница, следовательно ряд А расходится. Относительно ряда В). Так как коэффициенты 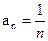убывают монотонно с ростом 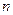и 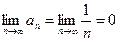, то есть выполнены оба условия признака Лейбница, ряд В) сходится. Но ряд 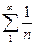расходится, следовательно ряд В) сходится условно.