Элементы операционного исчисления
Определение. Преобразованием Лапласа функции 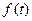 называется интеграл
называется интеграл 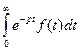 и обозначается
и обозначается 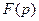 . Таким образом,
. Таким образом,
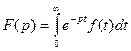 , где
, где
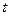 - действительная переменная,
- действительная переменная, 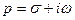 - комплексная переменная. При этом функция
- комплексная переменная. При этом функция 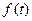 называется оригиналом,
называется оригиналом, 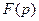 -изображением.
-изображением.
Условия, которым должен удовлетворять оригинал 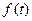 :
:
1) 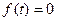 при
при 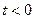
2) Не иметь знаменатель, который обращается в ноль. Например, функция  не может быть оригиналом.
не может быть оригиналом.
3) С возрастанием 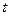 модуль функции
модуль функции 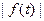 не может расти быстрее некоторой показательной функции, то есть,
не может расти быстрее некоторой показательной функции, то есть, 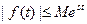 , где
, где  .
.
Например, функция 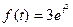 не может быть оригиналом, так как при любых числах
не может быть оригиналом, так как при любых числах 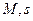 , данная функция растет быстрее чем функция
, данная функция растет быстрее чем функция 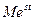 , то есть нарушается условие (3).
, то есть нарушается условие (3).
Свойство линейности изображения
Обозначим 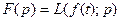 .Пусть оригиналы
.Пусть оригиналы 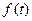 и
и 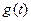 имеют изображения
имеют изображения 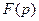 и
и 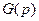 . Тогда
. Тогда 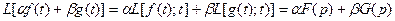 . Таким образом, изображением суммы
. Таким образом, изображением суммы 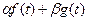 является
является 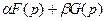 .
.
Пример 1. Найти изображение функции 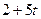 .
.
Решение. Имеем 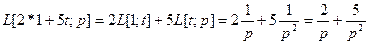 . Таким образом, изображением функции
. Таким образом, изображением функции 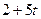 является
является 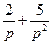 так, как изображением 1 согласно таблице является
так, как изображением 1 согласно таблице является 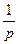 , а изображением
, а изображением 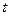 является
является 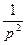 .
.
Пример 2. Найти изображение функции 3.
Решение. Имеем 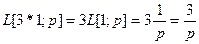 . Таким образом, изображением функции
. Таким образом, изображением функции 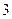 является
является 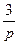 .
.
Пример 3. Какой оригинал соответствует изображению 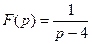 .
.
Решение. Согласно (4) таблицы изображений имеем при 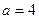 оригинал вида
оригинал вида
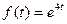
Пример 4. Найти изображение решения задачи Коши: 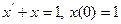
Решение. Имеем 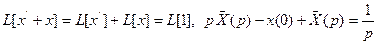 , где
, где
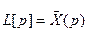
или 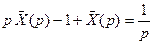 . Отсюда находим
. Отсюда находим 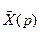 :
: 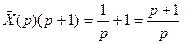 ,
,
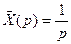 . Ответ:
. Ответ: 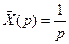
Пример5. Записать в изображениях решение задачи Коши вида
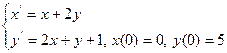
Решение. Имеем
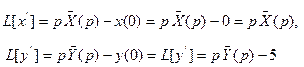
Далее 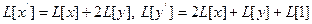 ,
, 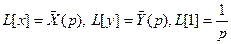 . Отсюда
. Отсюда
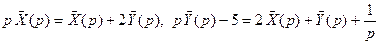
Ответ
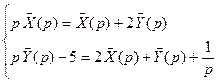
Таблица изображений
| Nпп | Оригинал 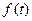 
| Изображение 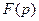
|
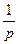
| ||
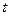
| 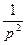
| |
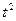
| 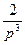
| |
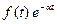
| 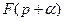
| |
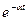
| 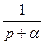
| |
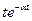
| 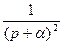
| |
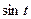
| 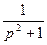
| |
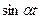
| 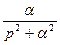
| |
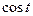
| 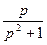
| |
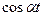
| 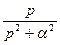
| |
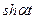
| 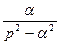
| |
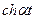
| 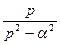
| |
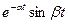
| 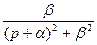
| |
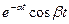
| 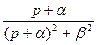
| |
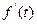 -производная -производная
| 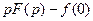 , где , где 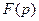 -изображение -изображение 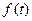
| |
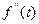 -вторая производная -вторая производная
| 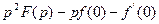 , где , где 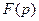 -изображение -изображение 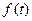
| |
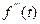 - третья производная - третья производная
| 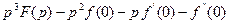
| |
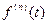 - - 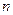 -я производная -я производная
| 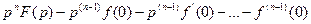
| |
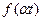
|  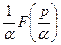
| |
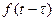
| 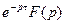
| |
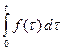
| 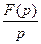
| |
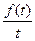
| 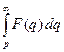
|
Дата добавления: 2015-10-13; просмотров: 758;
