Знакоположительные числовые ряды
Определение. Числовой ряд 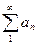 называется знакоположительным, если все
называется знакоположительным, если все  .
.
Рассмотрим знакоположительный ряд вида 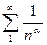 . (1)
. (1)
Ряд 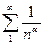 сходится , если
сходится , если 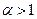 и расходится, если
и расходится, если 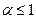 .
.
Примеры сходящихся рядов: 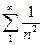 ,
, 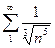 .
.
Примеры расходящихся рядов: 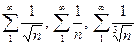 .
.
Примечание: По отношению к ряду 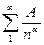 при
при 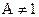 заключение о его поведении
заключение о его поведении
не изменяется, то есть, он сходится, если 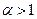 и расходится, если
и расходится, если 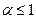 .
.
Рассмотрим ряд вида 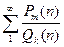 , (2)
, (2)
где 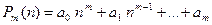 - многочлен степени m относительно переменного натурального n с действительными коэффициентами
- многочлен степени m относительно переменного натурального n с действительными коэффициентами 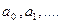 ,
,
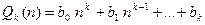 - многочлен степени k относительно переменного натурального n c действительными коэффициентами
- многочлен степени k относительно переменного натурального n c действительными коэффициентами 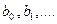
При этом числа 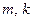 неотрицательные целые числа, не равные одновременно нулю.
неотрицательные целые числа, не равные одновременно нулю.
Например 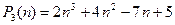 - многочлен степени 3,
- многочлен степени 3, 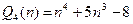 - многочлен степени 4.
- многочлен степени 4.
Утверждение. Если 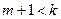 , (3)
, (3)
то ряд (2) сходится, в противном случае, то есть когда 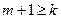 , (4)
, (4)
то ряд (2) расходится.
Пример. Ряд 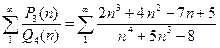 расходится, так как
расходится, так как 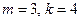 и выполнено условие (4).
и выполнено условие (4).
Пример. Ряд 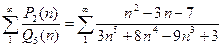 сходится, так как
сходится, так как 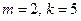 и выполнено условие (3).
и выполнено условие (3).
Пример. Ряд 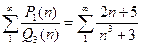 сходится, так как
сходится, так как 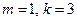 и выполнено условие (3).
и выполнено условие (3).
Пример. 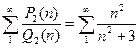 расходится, так как
расходится, так как 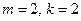 и выполнено условие (4).
и выполнено условие (4).
Пример. 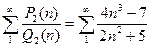 расходится, так как
расходится, так как 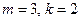 и выполнено условие (4).
и выполнено условие (4).
Пример. Найти 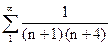 .
.
Решение.
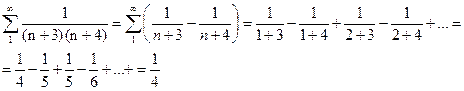
Признак сравнения. Пусть даны два знакоположитедьных ряда A) 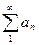 В)
В) 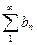 .
.
Если 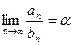 , где
, где 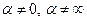 , то ряды А и В сходятся или расходятся одновременно.
, то ряды А и В сходятся или расходятся одновременно.
Пример. Указать сходящиеся числовые ряды.
1) 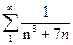 2)
2) 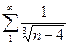 3)
3) 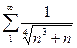 4)
4) 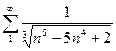
Решение. Для сравнения возьмем ряд 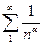 . Ясно, что в (1) надо взять
. Ясно, что в (1) надо взять 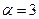 , в (2) надо взять
, в (2) надо взять 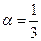 , в (3) надо взять
, в (3) надо взять 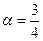 , в (4) надо взять
, в (4) надо взять 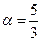 . Это делается из следующих соображений: В (1) отбрасывается слагаемое
. Это делается из следующих соображений: В (1) отбрасывается слагаемое 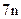 , в (2) отбрасывается -4, в (3) отбрасывается
, в (2) отбрасывается -4, в (3) отбрасывается 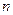 в (4) отбрасывается
в (4) отбрасывается 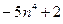 . После этого остаются ряды
. После этого остаются ряды 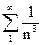 ,
,
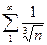 ,
, 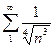 ,
, 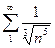 или после преобразований
или после преобразований 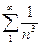 ,
, 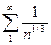 ,
, 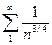 ,
, 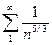 . Отсюда ряд (1) сходится так как,
. Отсюда ряд (1) сходится так как, 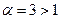 . Ряд (2) расходится так,как
. Ряд (2) расходится так,как 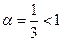 .
.
Ряд (3) расходится так,как  . Ряд (4) сходится так,как
. Ряд (4) сходится так,как 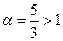 .
.
С использованием признака сравнения заключение о характере сходимости ряда 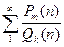
проводится следующим образом: в многочленах 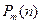 и
и 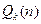 оставим старшие члены, то есть слагаемые
оставим старшие члены, то есть слагаемые 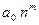 и
и 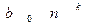 . В результате получим ряд
. В результате получим ряд 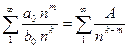 , где
, где 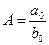 - постоянная. Отсюда при
- постоянная. Отсюда при 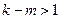 или то же самое
или то же самое 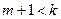 , ряд сходится
, ряд сходится
и при 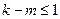 или
или 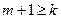 , ряд расходится.
, ряд расходится.
Дата добавления: 2015-10-13; просмотров: 845;
