Лекция 3. Числовые множества

Основные понятия:

Счетные множества; несчетные множества; числовые множества; ограниченным сверху (снизу) множества; верхняя (нижняя) грань множества; граничная точка множества; граница множества; комбинаторика; соединения; размещения; перестановки; сочетания; множество комплексных чисел; комплексное число; действительная часть комплексного числа; мнимая часть комплексного числа; число ; сложение комплексных чисел; умножение комплексных чисел; тригонометрическая форма комплексных чисел; абсолютная величина комплексного числа; аргумент комплексного числа; комплексно сопряженное число; формула Муавра.

Основные понятия

Будем рассматривать множества, элементами которых являются числа. Такие множества называются числовыми. Числовые множества задаются на оси действительных чисел R. На этой оси выбирают масштаб и указывают начало отсчета и направление. Наиболее распространенные числовые множества:

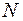· ‑ множество натуральных чисел;

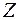· ‑ множество целых чисел;

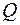· – множество рациональных или дробных чисел;

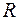· ‑ множество действительных чисел.

Множество всех рациональных чисел является счетным множеством. Счетным является множество всех точек плоскости (пространства) имеющих рациональные координаты.

Множество всех действительных чисел является несчетным: оно имеет мощность, называемую континуумом.

Некоторое непустое подмножество 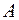множества действительных чисел называют ограниченным сверху (снизу), если существует действительное число 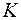такое, что 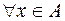выполняется неравенство ( ).

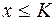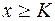Всякое число 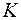с указанным свойством называют верхней (нижней) гранью множества .

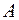Непустое подмножество 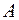множества действительных чисел называется ограниченным, если оно ограничено и сверху и снизу.

В противоположность этому определению, множество 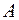называется неограниченным сверху (снизу), если какое бы число 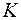мы бы не предложили в качестве верхней (нижней) границы множества 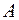, всегда найдется элемент этого множества, который будет больше (меньше) .

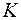Множество, неограниченное как сверху, так и снизу, называется неограниченным множеством.

Наименьшую из верхних граней непустого подмножества множества действительных чисел 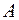называют точной верхней гранью этого множества и обозначают sup 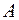. Наибольшую из нижних граней непустого подмножества множества действительных чисел 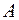называют точной нижней гранью этого множества и обозначают inf 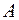. Символы sup и inf являются сокращениями от supremum (самый верхний) и infimum (самый нижний).

Примем без доказательства утверждение о том, что всякое ограниченное сверху (снизу) множество имеет точную верхнюю (нижнюю) грань.

Граничной точкой множества называется точка, у которой в любом содержащем ее открытом промежутке найдутся как точки, принадлежащие множеству, так и точки, не принадлежащие множеству. Сама граничная точка может, как принадлежать множеству, так и не принадлежать ему.

Граница множества – совокупность граничных точек множества:

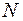· (множество натуральных чисел) ограниченно снизу (например, числом 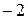) и не ограничено сверху;

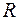· (множество действительных чисел) неограничено;

· множество отрицательных чисел неограничено снизу и ограничено сверху.