Сочетаниями из элементов по ( ) называют такие их соединения, каждое из которых содержит ровно данных элементов, и которые отличаются хотя бы одним элементом.

Рассмотрим все допустимые сочетания элементов .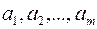

Делая в каждом из них 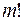возможных перестановок их элементов, очевидно, получим все размещения из 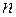элементов по :

.

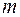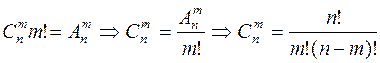Числа 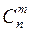являются коэффициентами в формуле бинома Ньютона:

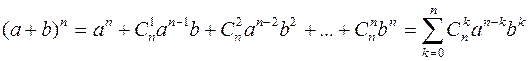
Свойства сочетаний:

1.

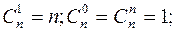
2.

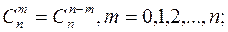
3.

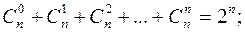
4.

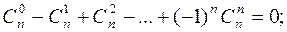
5.

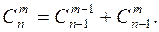
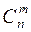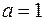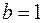Свойства 1 и 2 очевидно следуют из определения , свойства 3 и 4 доказываются с помощью бинома Ньютона, полагая для свойства 3 что и , а для свойства 4 что 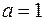и 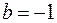. Свойство 5 можно проверить следующим образом:

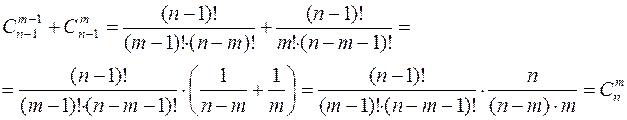
Это свойство позволяет последовательно вычислять биномиальные коэффициенты 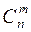с помощью так называемого треугольника Паскаля:

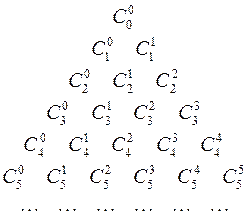
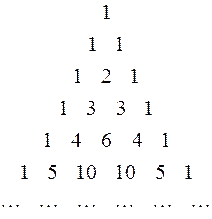
Здесь каждое число, кроме крайних единиц, является суммой двух вышерасположенных.