Отношения эквивалентности и упорядоченности

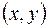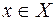В математике понятие отношения используется для обозначения какой-либо связи между объектами. Отношение есть некоторое множество упорядоченных пар , где , а .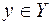

v Отношение называется рефлексивным, если каждый элемент множества находится в этом отношении сам с собой ( ).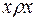

v Отношение называется симметричным, если оно обладает свойством коммутативности ( ).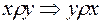

v Отношение называется транзитивным, если .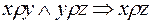

v Отношение называется антисимметричным, если .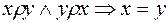

Часто приходится рассматривать несколько элементов множества как эквивалентные, потому что по определенным признакам один элемент может быть заменен другим. Так, например, по признаку величины дроб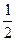и и 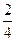эквивалентны. Отношение эквивалентности рефлексивно, симметрично и транзитивно. Понятие эквивалентности подразумевает выполнение следующих условий:

· каждый элемент эквивалентен самому себе;

· высказывание, что два элемента являются эквивалентными, не требует уточнения, какой из элементов рассматривается первым;

· два элемента, эквивалентные первому, эквивалентны между собой.

Пусть 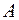– множество, в котором определено отношение эквивалентности. Подмножество элементов, эквивалентных элементу 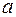, называется классом эквивалентности: все элементы этого класса эквивалентны между собой и всякий элемент 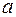из 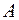находится в одном и только в одном классе (если элементов, эквивалентных 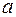, не существует, то 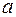может быть и единственным элементом класса). Отношение эквивалентности в 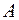определяет на 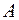разбиение на классы эквивалентности, т.е. 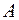становится объединением непересекающихся классов.

Особенности природы элементов множества в большинстве случаев позволяют установить между ними отношения полного (или совершенного) порядка. Это отношение по определению обладает следующими свойствами:

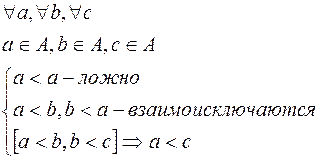
Если между элементами множества определено также и отношение эквивалентности, то между элементами устанавливается отношение неполного или нестрогого порядка:

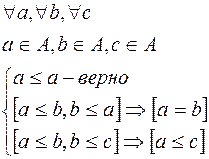
Возможны случаи, когда некоторые элементы множества не сравнимы. Такие множества называются частично упорядоченными.

Контрольные вопросы к лекции №2

1. Понятие множества.

2. Основные операции над множествами.

3. Понятие отображения.

4. Понятие области определения отображения.

5. Охарактеризовать по отдельности инъективное, сюръективное и биективное отображения.

6. Понятие мощности множества.

7. Сравнение бесконечных множеств.

8. Счетные и несчетные множества.

9. Понятие эквивалентности.

10. Охарактеризовать упорядоченные и частично упорядоченные множества.