Числовые ряды
Определение. Бесконечная сумма вида 
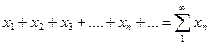 , где (1)
, где (1)
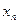 - общий член ряда (произвольное число, как положительное так и отрицательное), называется числовым рядом.
- общий член ряда (произвольное число, как положительное так и отрицательное), называется числовым рядом.
Определение. Ряд (1) сходится , если сходится последовательность частичных сумм ряда

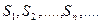 , то есть
, то есть 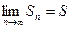 , где
, где 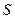 -конечное число, называемое суммой сходящегося ряда, а
-конечное число, называемое суммой сходящегося ряда, а 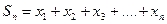 - частичная сумма ряда (1).
- частичная сумма ряда (1).
Утверждение. Из сходимости ряда (1) вытекает, что 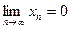 . Отсюда получаем, что
. Отсюда получаем, что
если 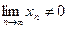 , то ряд (1) расходится.
, то ряд (1) расходится.
Рассмотрим ряд в виде геометрической прогрессии : 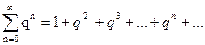 , где
, где 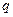 - некоторое число. При
- некоторое число. При 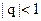 или
или 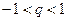 г.п. сходится и сумма ее равна
г.п. сходится и сумма ее равна 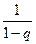 , при
, при 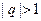 , расходится.
, расходится.
Пример. Найти 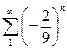 .
.
Решение. 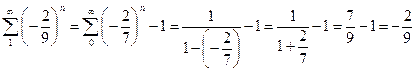 . Здесь
. Здесь 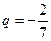 .
.
Пример. Найти сумму числового ряда 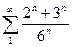 .
.
Решение. 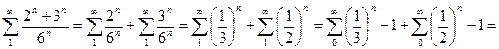
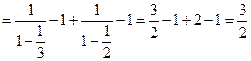
Дата добавления: 2015-10-13; просмотров: 499;
