Приложения определённого интеграла
Вычисление площади в прямоугольных координатах
Площадь криволинейной трапеции, ограниченной
кривой y=f(x), 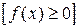 , прямыми x=a и x=b и осью Ох находится по формуле
, прямыми x=a и x=b и осью Ох находится по формуле
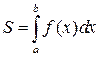 .
.
Пример.Найти площадь фигуры, ограниченной кривой 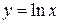 , прямой
, прямой 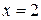 и осью абсцисс.
и осью абсцисс.
Решение. Построим фигуру, ограниченную указанными линиями:
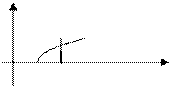
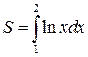 .
.
Применим метод интегрирования по частям, полагая 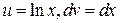 , тогда
, тогда 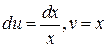 .
.
Подставляем в формулу интегрирования по частям:
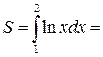
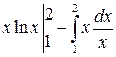 =
= 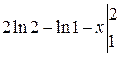 =
=
= 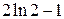 .
.
Площадь фигуры, ограниченной кривыми y=f(x), y=g(x) и прямыми x=a, x=b, причем 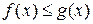 , находится по формуле
, находится по формуле
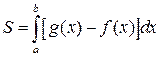 .
.
Площадь фигуры, ограниченной кривыми 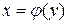 ,
, 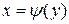 и прямыми у=с, у=d, причем
и прямыми у=с, у=d, причем 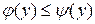 , находится по формуле
, находится по формуле
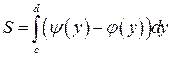 .
.
Пример.Найти площадь фигуры, ограниченной прямой 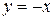 и параболой
и параболой 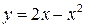 .
.
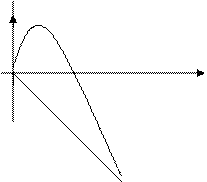
Решение. Находим точки пересечения прямой и параболы и строим ограниченную ими фигуру:
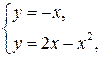
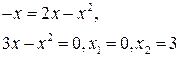
 |
Дата добавления: 2015-10-13; просмотров: 651;
