Знакочередующиеся ряды. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Ряд 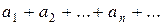 называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Признак сходимости знакопеременного ряда.Если ряд 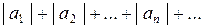 , составленный из абсолютных величин членов знакопеременного ряда, сходится, то и исходный ряд сходится.
, составленный из абсолютных величин членов знакопеременного ряда, сходится, то и исходный ряд сходится.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин членов данного ряда.
Сходящийся знакопеременный ряд называется условно сходящимся, если ряд, составленный из абсолютных величин его членов, расходится.
Ряд вида
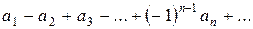 ,
,
где 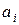 – положительные числа, называется знакочередующимся.
– положительные числа, называется знакочередующимся.
| Признак Лейбница. | Знакочередующийся ряд сходится, если его члены монотонно убывают по абсолютной величине и модуль общего члена стремится к нулю при 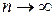 , т.е. , т.е. 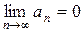 . .
|
Пример. Исследовать на сходимость ряд 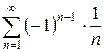 .
.
Решение. Находим: 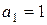 ,
, 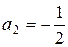 ,
, 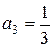 ,
, 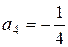 .
.
1) Члены ряда монотонно убывают по абсолютной величине: 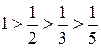 .
.
2) 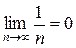 .
.
Условия сходимости знакочередующегося ряда выполняются, значит данный ряд сходится.
| 9. Степенные ряды |
Ряд 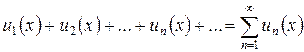 , членами которого являются функции от
, членами которого являются функции от 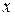 называется функциональным.
называется функциональным.
Функциональный ряд называется сходящимся в точке 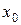 , если при
, если при 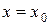 он обращается в сходящийся числовой ряд.
он обращается в сходящийся числовой ряд.
Функциональный ряд называется расходящимся в точке 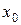 , если при
, если при 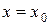 он обращается в расходящийся числовой ряд.
он обращается в расходящийся числовой ряд.
Множество значений 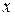 , при которых функциональный ряд сходится, называется областью сходимости функционального ряда.
, при которых функциональный ряд сходится, называется областью сходимости функционального ряда.
Функциональный ряд вида
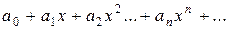
или
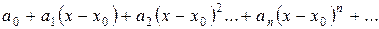 ,
,
где 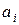 – числа, называемые коэффициентами, называется степеннымрядом.
– числа, называемые коэффициентами, называется степеннымрядом.
Ряд, который сходится при любом значении 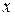 , называется всюдусходящимся.
, называется всюдусходящимся.
Дата добавления: 2015-09-28; просмотров: 691;
