Сходимости числового ряда

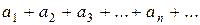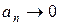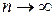Если ряд сходится, то его общий член при , т.е.

.

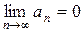! Этот общий признак не является достаточным, т.е. из того, что общий член стремиться к нулю при 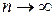, нельзя сделать вывод о сходимости ряда. Но если общий член не стремится к нулю, то ряд расходится.

Пример. Исследовать на сходимость ряд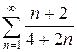

Решение. Проверим, выполняется ли необходимое условие сходимости ряда, а именно 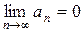. В наше случае 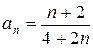, тогда

.

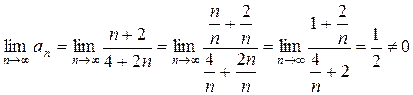Так как необходимое условие не выполняется, то этот ряд расходится.

Ряд, членами которого являются только положительные числа, называется знакоположительным.