Область сходимости степенного ряда.

Степенной ряд имеет вид: (все параметры комплексные). В дальнейшем без ограничения общности:

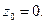
Теорема (Первая теорема Абеля). Если ряд (*) сходится в точке 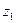, то он сходится равномерно внутри круга: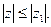

Доказательство. Имеем 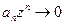(общий член ряда ; необходимое условие сходимости ряда). В частности, 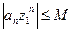. Фиксируем 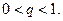И рассмотрим: 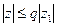(любой круг строго меньший). Тогда 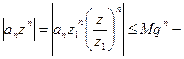убывающая геометрическая прогрессия (по признаку сравнения ряд сходится тогда равномерно).

Следствие. Областью сходимости степенного ряда является некоторый круг. Назовём 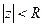- радиусом сходимости.

Замечание. Не исключаются случаи, когда R = 0 (расходится везде кроме одной точки) или 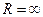(везде сходится).

Пример. 1) 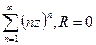расходится везде кроме 0.

2)

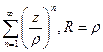
3) 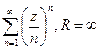по признаку Деламбера, сходящийся ряд.

Замечание. На границе области сходимости поведение ряда может быть любым.

Пример. R = 1 – единичная окружность.

1) расходится на единичной окружности.

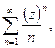
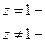
2) 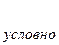на единичной окружности.

3) 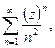сходится абсолютно и равномерно на единичной окружности.

4) 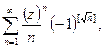сходится условно во всех точках на окружности.

Теорема (Формула Коши-Адамара). Радиус сходимости вычисляется так: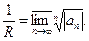

Доказательство. 1) Пусть 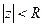. Мы должны доказать, что ряд тогда сходится. Напишем: 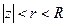, тогда 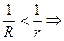начиная с некоторого номера: 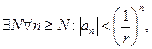а тогда 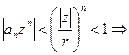по признаку сравнения ряд сходится.

2) Пусть . Мы должны доказать, что ряд тогда расходится. 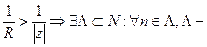подпоследовательность натурального ряда.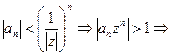

по признаку сравнения ряд расходится.

Утверждение. 1) Степенной ряд сходится к функции, голоморфной в круге сходимости.

2) Степенной ряд является рядом Тейлора для своей суммы. .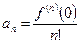

Доказательство. 1) По первой теореме Абеля ряд сходится равномерно внутри круга сходимости. По первой теореме Вейерштрасса его сумма голоморфна, следовательно всё клёво.

2) 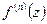По первой теореме Вейерштрасса можно ряд дифференцировать почленно. Т.е. 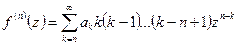. Подставим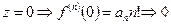

Утверждение (Переформулировка). В степенной ряд можно разложить только голоморфную функцию, при этом единственным образом – только в ряд Тейлора.

Пример. 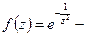нельзя разложить в степенной ряд в окрестности 0. Т.к. она не голоморфна в 0.

Теорема (Вторая теорема Абеля). Если степенной ряд сходится в точке 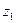, то он сходится равномерно на [0, z₁].

Доказательство. Сведём теорему к признаку сходимости числовых рядов. Без ограничения общности 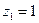(замена переменных), тогда 1. 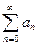- сходится.

2. 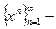равномерно ограничена на [0, 1].

3. 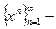не возрастающая, а тогда это признак Коши.

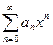сходится равномерно на [0, 1].