Знакоположительных рядов
| Признак Даламбера. | Если для положительного ряда существует 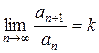 , то , то
|
§ при 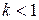 ряд сходится,
ряд сходится,
§ при 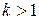 ряд расходится,
ряд расходится,
§ при 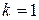 о сходимости ряда сказать ничего нельзя, т.е. надо применять другой признак.
о сходимости ряда сказать ничего нельзя, т.е. надо применять другой признак.
Пример. Исследовать на сходимость ряд
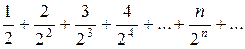
Решение. Находим 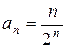 ,
, 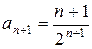 .
.
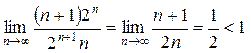 – ряд сходится.
– ряд сходится.
| Интегральный признак Коши. | Ряд с положительными членами 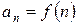 сходится или расходится одновременно с несобственным интегралом сходится или расходится одновременно с несобственным интегралом
|
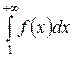 ,
,
где 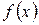 – непрерывная, положительная, монотонная убывающая производящая функция.
– непрерывная, положительная, монотонная убывающая производящая функция.
Пример. Исследовать на сходимость гарнмонический ряд 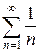 .
.
Решение. Вычислим
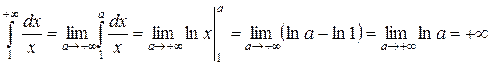 .
.
Гармонический ряд расходится.
Пример.Исследовать на сходимость ряд 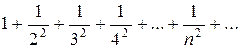
Решение. Члены ряда можно рассматривать как значения функции 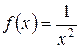 при
при 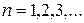 Члены ряда убывают:
Члены ряда убывают: 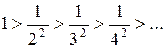 Вычислим
Вычислим
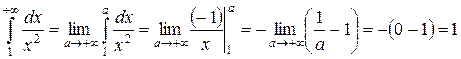 .
.
Несобственный интеграл сходится, значит сходится и данный ряд.
| Радикальный признак Коши. | Если для положительного ряда существует 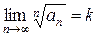 , то , то
|
§ при 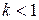 ряд сходится,
ряд сходится,
§ при 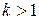 ряд расходится,
ряд расходится,
§ при 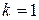 о сходимости ряда сказать ничего нельзя.
о сходимости ряда сказать ничего нельзя.
(Этот признак применяется лишь тогда, когда 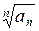 извлекается).
извлекается).
Пример. Исследовать на сходимость 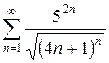
Решение. Преобразуем выражение под знаком суммы.
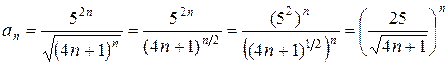
Применяя радикальный признак Коши, имеем:
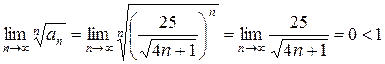
Таким образом, исходный ряд сходится.
| Первый признак сравнения. | Сравним ряд с положительными членами
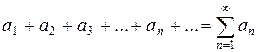 с другим знакоположительным рядом
с другим знакоположительным рядом
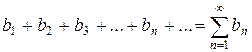
|
§ если ряд 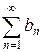 сходится и начиная с некоторого члена ряда выполняется неравенство
сходится и начиная с некоторого члена ряда выполняется неравенство 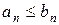 , то ряд
, то ряд 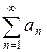 также сходится;
также сходится;
§ если ряд 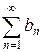 расходится и начиная с некоторого члена ряда выполняется неравенство
расходится и начиная с некоторого члена ряда выполняется неравенство 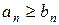 , то и ряд
, то и ряд 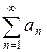 также расходится.
также расходится.
Пример. Исследовать сходимость ряда 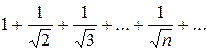
Решение. Сравним данный ряд с гармоническим рядом
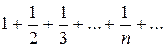
Т.к. каждый член исходного ряда, начиная со второго, больше соответствующего члена гармонического ряда, а гармонический ряд является расходящимся (интегральный признак), то данный ряд тоже расходится.
Замечание. Обобщенный гармонический ряд 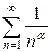 при
при 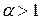 сходится, при
сходится, при 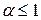 расходится.
расходится.
| Второй признак сравнения. | Даны два положительных ряда 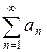 и и 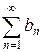 . Если существует конечный предел отношения членов ряда при . Если существует конечный предел отношения членов ряда при 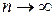 , отличный от нуля, то оба ряда сходятся, либо расходятся одновременно, т.е. , отличный от нуля, то оба ряда сходятся, либо расходятся одновременно, т.е.
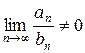 и и 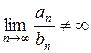 . .
|
Пример. Исследовать ряд на сходимость 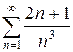 .
.
Решение. Сравним этот ряд со сходящимся рядом 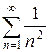 (он сходится по интегральному признаку). Проверим, существует конечный, отличный от нуля предел
(он сходится по интегральному признаку). Проверим, существует конечный, отличный от нуля предел
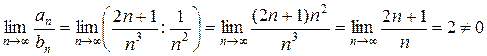 .
.
Таким образом, ряд является сходящимся.
Дата добавления: 2015-09-28; просмотров: 813;
