сходимости степенного ряда

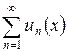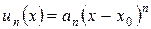Для степенного ряда , где , составим предел модуля отношения последующего члена ряда к предыдущему

.

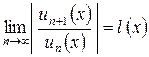Для всех 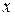, при которых:

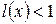§ , ряд сходится,

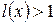§ , ряд расходится,

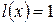§ , необходимы дополнительные исследования.

Пример. Определить интервал сходимости степенного ряда .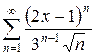

Решение. Запишем общий член ряда и следующий:

; .

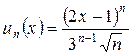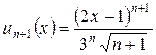Найдем предел отношения их абсолютных величин:

.

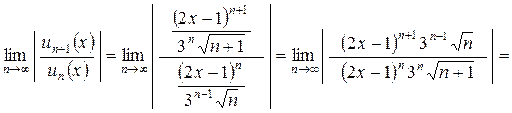
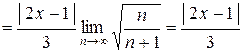Найдем интервал сходимости из условия .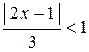

, , ,

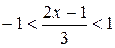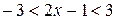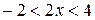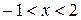
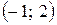– интервал сходимости.

Для нахождения области сходимости проверим сходимость ряда на концах интервала сходимости.

: .

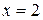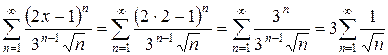Полученный знакоположительный ряд расходится (см. стр. 57), следовательно, точка 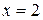не входит в область сходимости.

: .

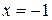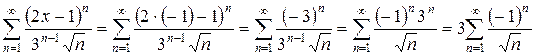Для полученного знакочередующегося ряда выполняются оба условия теоремы Лейбница:

1)

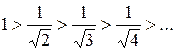
2) .

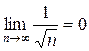Ряд сходится. Точка 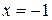входит в область сходимости.

Итак, область сходимости данного ряда: .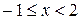

ЛиТЕРАТУРА

1. Зайцев И.А. Высшая математика. – М.: Высшая школа, 1991.

2. Карасев А.И и др. Математика для экономистов. – М.: Высшая школа, 1987.

3. Кудрявцев В.А., Демидович В.П. Краткий курс высшей математики. – М.: Наука, 1985.

4. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1989.

5. Натансон И.И. Краткий курс высшей математики. – М.: Наука, 1968.

6. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. – М.: Наука, т.1,2, 1985.