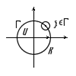Особые точки на границе круга сходимости.

Дан степенной ряд: 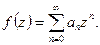Обозначим R – радиус сходимости этого ряда. Предположим: Обозначим: U – круг, где сходится, Г – граница круга. Зафиксируем точку на границе круга сходимости.

Определение. Точка 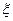называется правильной точкой степенного ряда, если функция 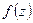аналитически продолжается в некоторую окружность этой точки.

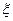Точка называется особой точкой степенного ряда, если она не является правильной.

Замечание. Из определения следует, что правильные точки образуют открытое

множество на окружности Г. А особые точки – замкнутое.

Утверждение. На границе круга сходимости есть хотя бы одна особая точка.

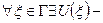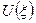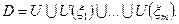Доказательство. Предположим обратное. Т.е. все точки – правильные. Тогда у каждой точки окрестность: f – аналитически продолжается в . Из открытого покрытия компакта Г выберем конечное подпокрытие: И рассмотрим: Имеем 2 свойства: 1) f – аналитически продолжается в области D (по теореме единственности) 2) 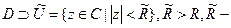ближайший к началу координат. 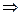противоречие с тем, что круг сходимости степенного ряда совпадает с максимальным кругом голоморфности его суммы ( 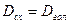) предположение не верно. утверждение.