Тема 4.3 Отношения между множествами.

В математике изучают не только те или иные множества, но и отношения , взаимосвязи между ними. Например, нам известно, что все натуральные числа являются целыми. Понятие множества позволяет обобщить конкретные случаи взаимосвязи между различными совокупностями, позволяет посмотреть на них с единой точки зрения.

Если множества А и В имеют общие элементы, т.е. элементы принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.

Например, если A={a,b,c,d,e} , B={b,d,k,m}, C={x,y,z}, то можно утверждать, что множества А и В пересекаются, так как имеют общие элементы b и d, а множества А и С, В и С не пересекаются, поскольку не имеют общих элементов.

Рассмотрим теперь множества A={a,b,c,d,e} и B={c,d,e}. Они пересекаются, и, кроме того, каждый элемент множества В является элементом множества А. в этом случае говорят, что множество В включается в множество А или множество В являетсяподмножеством множества А и пишут .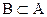

Определение.Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.

Рассмотрим теперь множества A={a,b,c,d,e} и B={c,a,b,d,e}. Они пересекаются, и каждый элемент множества А является элементом множества В, т.е. В 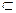А. в этом случае говорят, что множества А и В равны и пишут А=В.

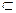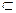Определение.Множества А и В называются равными, если А В и В А.

Отношения между множествами наглядно представляют при помощи особых чертежей, называемых кругами Эйлера. Для этого множества представляют в виде кругов, овалов или любых других геометрических фигур.

А В А В

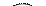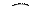а) б) в) г)

а) изображение множеств, если у них есть общие элементы, и если ни одно из них не является подмножеством другого.

б) если множество В является подмножеством множества А, то круг изображающий множество В целиком помещают в круг изображающий множество А

в) если множество А является подмножеством множества В, то круг изображающий множество А целиком помещают в круг изображающий множество В.

Г) изображение равных множеств.