Тема 6.2 Правило Крамера для систем линейных уравнений.
Система m линейных уравнений с n переменными имеет вид:
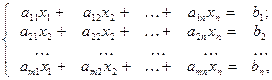
где а11, а12, …аmn и b1, b2,…,bn- произвольные числа, называемые соответственно коэффициентами при переменных и свободными членами уравнений.
Решением системы называется такая совокупность n чисел (x1=k1, x2=k2, …,xn=kn) при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Пусть число уравнений системы равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а определитель 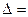 |A| называется определителем системы. Существует метод решения таких систем по правилу Крамера.
|A| называется определителем системы. Существует метод решения таких систем по правилу Крамера.
Теорема Крамера. Пусть 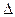 - определитель матрицы системы А, а
- определитель матрицы системы А, а 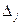 - определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если
- определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если 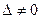 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
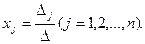
Пример. Решить систему линейных уравнений по правилу Крамера .
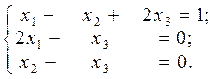
Решение :
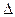 =
= 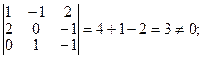
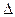 1=
1= 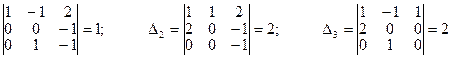
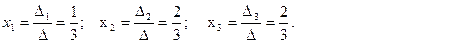
Ответ: ( 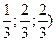 .
.
Дата добавления: 2015-11-04; просмотров: 613;
