Тема 4.1 Понятие множества и элементы множества.

В математике часто рассматриваются те или иные группы объектов как единое целое: натуральные числа, треугольники, квадраты и т.д. все эти различные совокупности называют множествами.

Понятие множества является одним из основных понятий и поэтому не определяется через другие. Его можно пояснить на примерах. Так, можно говорить о множестве гласных букв русского алфавита, о множестве натуральных чисел, о множестве треугольников.

Математический смысл слова « множество» отличается от того, как оно используется в обыденной речи, где его связывают с большим количеством предметов. В математике этого не требуется. Здесь можно рассматривать множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.

Множество принято обозначать прописными буквами латинского алфавита: A,B,C,…,Z .

Множество, не содержащее ни одного объекта, называется пустыми обозначается символом .

Объекты, из которых образовано множество, называют элементами.

Элементы множества принято обозначать строчными буквами латинского алфавита: a,b,c,…,z.

Предложение « Объект а принадлежит множеству А» можно записать, используя символы: 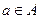. Предложение « Объект а не принадлежит множеству А» можно записать, используя символы: .

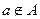Множества бывают конечныеи бесконечные.Эти понятия мы принимаем без определения.

Для ряда числовых множеств приняты стандартные обозначения:

N- множество натуральных чисел;

Z -множество целых чисел;

Q– множество рациональных чисел;

R - множество действительных чисел.