Тема 6.1 Матрицы и определители.
В математике существует ещё одно множество, элементами которого являются так называемые матрицы. Структуры, которыми наделено это множество, оказывается очень удобным аппаратом решения ряда алгебраических задач, в частности решения систем линейных уравнений.
Матрицей называется прямоугольная таблица чисел , состоящая из m строк и n столбцов: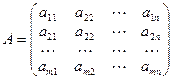 
.
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными( заглавными) буквами латинского алфавита, например, А, В, С, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: aij, где i- номер строки, j- номер столбца. Цифры m и n указывают размерность матрицы.
Если m=n, то матрица называется квадратной. Например,
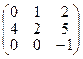- квадратная матрица размерности 3.
Операции над матрицами.
1) Матрицы одинаковых размерностей можно складывать( суммируя элементы с одинаковыми индексами).Матрицы можно умножать на число ( умножая все элементы матрицы на это число).
Пример. Сложить матрицы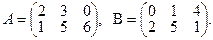 
Решение :
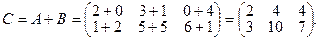
2) Матрицы можно умножать на число ( умножая все элементы матрицы на это число).
Пример. Умножить матрицу А на число 5.
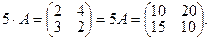
3) Матрицу А можно умножить на матрицу В, когда число столбцов первой матрицы равно числу строк второй ( произведением матриц будет называться матрица, каждый элемент, которой равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В).
Пример . вычислить произведение матриц А.В, где
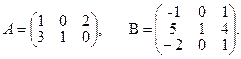
Решение:
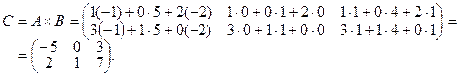
Для квадратных матриц вводится понятие определителя- числа, характеризующего квадратную матрицу А. Определитель матрицы А обозначается |A| или 
.
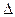Определителем первого порядка, называется элемент a11:
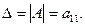Например. А=(3), тогда |A|=3.
Определителем второго порядка, называется число, которое вычисляется по формуле:
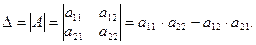
Например . Вычислить определитель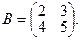 
Решение:
= 
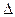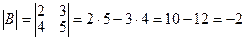
Определителем третьего порядка называется число, которое вычисляется по правилу треугольника (рис. 21):
а11 а12 а13
а21 а22 а23
а31 а32 а33
+ рис. 21 -
Например. Вычислить определитель
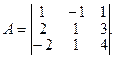
Решение :
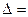
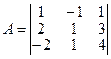=1.1.4+2.1.1+(-1)3(-2)-1.1(-2)-1.3.1-2(-1)4=
=4+2+6+2-3+8=19.
Ответ :19.
Дата добавления: 2015-11-04; просмотров: 555;