Базисный минор матрицы. Ранг матрицы.

Как было сказано выше, минором матрицы порядка s называется определитель матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких-либо выбранных s строк и s столбцов.

Определение. В матрице порядка m´n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе, т.е. r совпадает с меньшим из чисел m или n.

Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными.В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

Определение. Порядок базисного минора матрицы называется рангомматрицы и обозначается Rg А.

Очень важным свойством элементарных преобразований матриц является то, что они не изменяют ранг матрицы.

Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.

Надо отметить, что равные матрицы и эвивалентные матрицы — понятия совершенно различные.

Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.

Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.

Пример. Определить ранг матрицы.

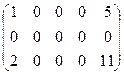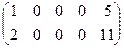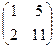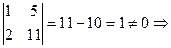~ ~ , RgA = 2

Пример. Определить ранг матрицы.

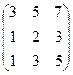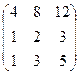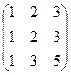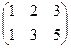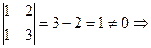~ ~ ~ , Rg = 2.

Пример. Определить ранг матрицы.

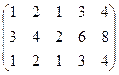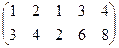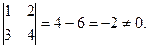~ , Þ Rg = 2.

Если с помощью элементарных преобразований не удается найти матрицу, эквивалентную исходной, но меньшего размера, то нахождение ранга матрицы следует начинать с вычисления миноров наивысшего возможного порядка. В вышеприведенном примере – это миноры порядка 3. Если хотя бы один из них не равен нулю, то ранг матрицы равен порядку этого минора.

1.8 Теорема о базисном миноре

Теорема.В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.

Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.

Если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю.