Элементарные преобразования систем
К элементарным преобразованиям относятся:
1) Прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на одно и то же число, не равное нулю.
2) Перестановка уравнений местами.
3) Удаление из системы уравнений, являющихся тождествами для всех х.
1.12 Теорема Кронекера – Капелли
Леопольд Кронекер (1823-1891) — немецкий математик.
Теорема:Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
RgA = RgA*.
Очевидно, что система (1) может быть записана в виде:
x1 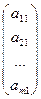 + x2
+ x2  + … + xn
+ … + xn 
Доказательство.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример. Определить совместность системы линейных уравнений:

A = 
~ 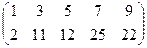 .
.  RgA = 2.
RgA = 2.
A* = 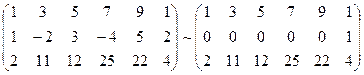 RgA* = 3.
RgA* = 3.
Система несовместна.
Пример. Определить совместность системы линейных уравнений.
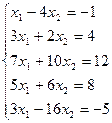 А =
А = 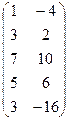 ;
; 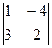 = 2 + 12 = 14 ¹ 0; RgA = 2;
= 2 + 12 = 14 ¹ 0; RgA = 2;
A* = 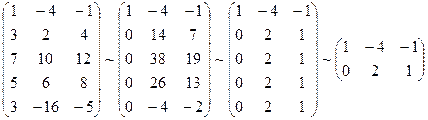
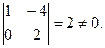 RgA* = 2.
RgA* = 2.
Система совместна. Решения: x1 = 1; x2 =1/2.
Дата добавления: 2015-10-13; просмотров: 882;
